Решение кубических уравнений - калькулятор
Кубическое уравнение - это уравнение вида:
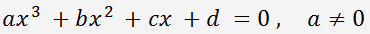
Коэффициенты
a,
b,
c и
d - вещественные числа и a ≠ 0.
Решение кубического уравнения
Чтобы найти корни кубического уравнения с помощью калькулятора кубических уравнений, введите коэффициенты
a,
b,
c и
d и нажмите кнопку 'Решить'.
Ниже приведены примеры решения кубических уравнений с помощью калькулятора кубических уравнений.
Рассмотрим уравнение
x3 - 4x2 + x + 6 = 0.
В данном уравнении коэффициент при x³ равен 1, поэтому соответствующее поле можно оставить пустым или ввести в него 1 (a = 1).
В поле для коэффициента при x² введите -4 (b = -4).
Коэффициент при x можно оставить пустым или написать 1 (c = 1).
В поле свободного члена введите 6 (d = 6).
Рассмотрим уравнение
10x3-6x2 = 0.
В данном уравнении коэффициент при x и свободный член равны нулю.
Значения коэффициентов должны быть заполнены следующим образом а = 10, b = -6, c = 0, d = 0.
Поле свободного члена d можно оставить пустым.
Коэффициент с надо обязательно поставить равным 0. Если оставить данное поле пустым, то коэффициент с будет считаться равным 1, и получится другое уравнение 10x
3 - 6x
2 + x= 0.
Решение кубического уравнения по формуле Кардано
Приведем уравнение к каноническому виду:
Разделим уравнение на
a
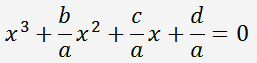
и сделаем замену переменных
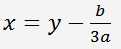
.
Получаем уравнение
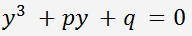
, где
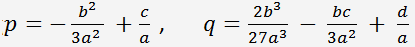
.
Обозначим дискриминант кубического уравнения
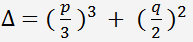
.
По формулам Кардано 3 корня уравнения определяются следующим образом:
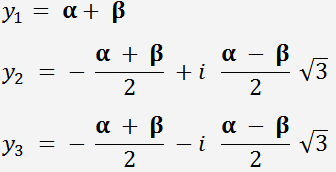
,
где
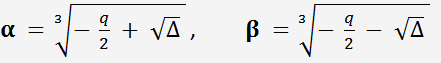
При этом для каждого
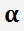
выбирается такое
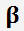
, что
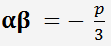
.
Количество корней уравнения определяются следующим образом:
Если
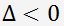
, уравнение имеет три действительных корня.
Если
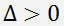
, уравнение имеет один действительный и два комплексно сопряженных корня.
Если
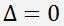
, уравнение имеет два действительных корня. Если p = q = 0, уравнение имеет один действительный корень.

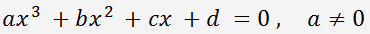
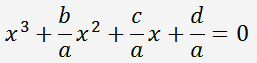
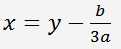 .
.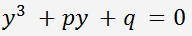 , где
, где 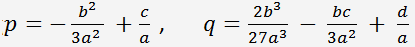 .
.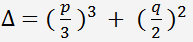 .
.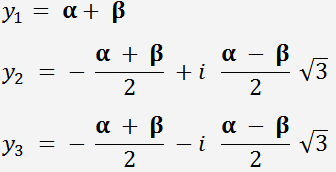 ,
,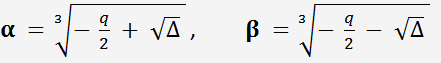
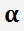 выбирается такое
выбирается такое 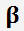 , что
, что 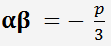 .
.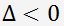 , уравнение имеет три действительных корня.
, уравнение имеет три действительных корня.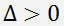 , уравнение имеет один действительный и два комплексно сопряженных корня.
, уравнение имеет один действительный и два комплексно сопряженных корня.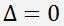 , уравнение имеет два действительных корня. Если p = q = 0, уравнение имеет один действительный корень.
, уравнение имеет два действительных корня. Если p = q = 0, уравнение имеет один действительный корень.