Решение уравнений четвертой степени - калькулятор
Чтобы найти корни уравнения 4-ой степени с помощью калькулятора, введите коэффициенты
a,
b,
c,
d и
e и нажмите кнопку 'Решить'.
Решение уравнения 4-ой степени (методом Феррари)
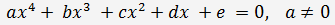
(1)
1. С помощью замены
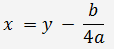
приходим к приведенному уравнению
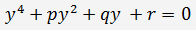
(2),
где
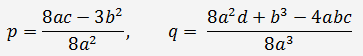
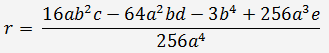
2. Если
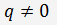
, то решаем вспомогательное кубическое уравнение
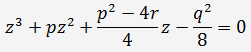
Если
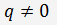
, то у этого уравнения всегда существует положительный корень, обозначим его
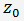
.
Тогда корни исходного уравнения (1) можно получить по формулам
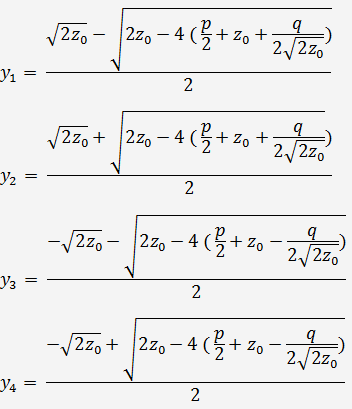
3. Если q = 0, то приведенное уравнение (2) становится биквадратным
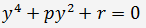
И четыре корня этого уравнения можно получить по формулам
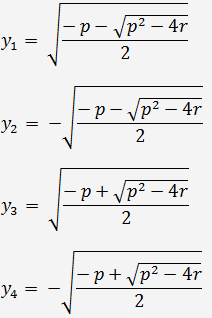
4. Оценить погрешность решения можно с помощью соответствующих невязок
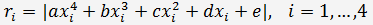
чем меньше величины
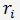
, тем точнее решение. Для более точной оценки имеет смысл рассмотреть относительную погрешность.
Для этого нужно решить уравнение
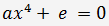
и вычислить соответствующие невязки
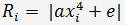
Тогда относительные невязки
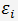
можно найти по формулам
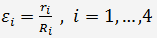
.

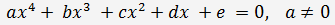 (1)
(1)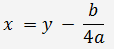 приходим к приведенному уравнению
приходим к приведенному уравнению 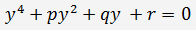 (2),
(2),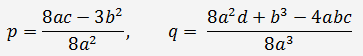
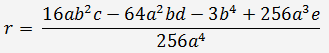
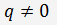 , то решаем вспомогательное кубическое уравнение
, то решаем вспомогательное кубическое уравнение 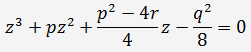
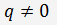 , то у этого уравнения всегда существует положительный корень, обозначим его
, то у этого уравнения всегда существует положительный корень, обозначим его 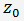 .
.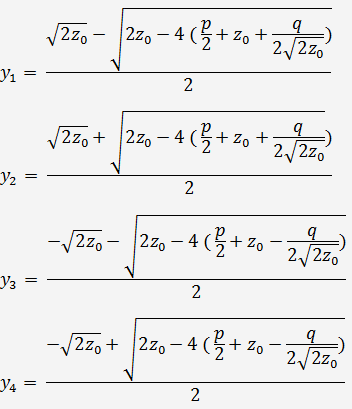
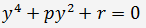
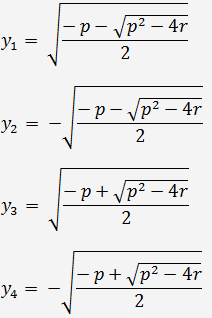
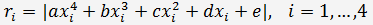
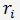 , тем точнее решение. Для более точной оценки имеет смысл рассмотреть относительную погрешность.
, тем точнее решение. Для более точной оценки имеет смысл рассмотреть относительную погрешность.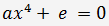 и вычислить соответствующие невязки
и вычислить соответствующие невязки 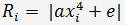
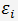 можно найти по формулам
можно найти по формулам 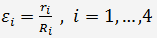 .
.