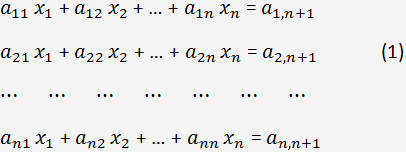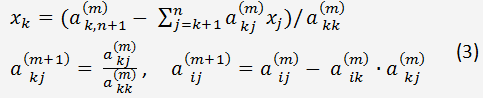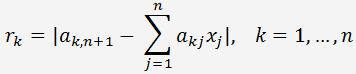Решение систем линейных уравнений

Решение системы n линейных уравнений с n неизвестными - калькулятор

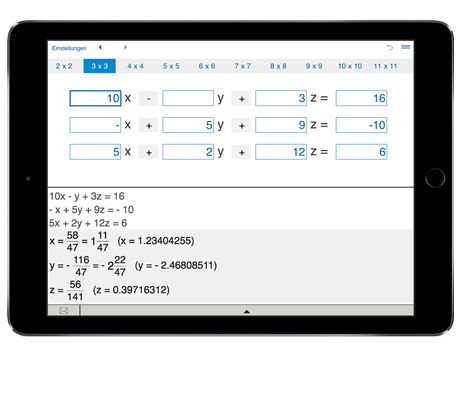
Универсальный калькулятор позволяет быстро и легко решать системы n линейных уравнений с n неизвестными. Для решения СЛАУ необходимо задать количество уравнений и ввести соответствующие коэффициенты.

Возможности универсального калькулятор: решение систем уравнений с двумя неизвестными, тремя неизвестными, 4 неизвестными, 5 неизвестными, 6 неизвестными, 7 неизвестными, 8 неизвестными, 9 неизвестными, 10 неизвестными и 11 неизвестными.

Решение систем линейных алгебраических уравнений методом Гаусса

Численное решение систем линейных алгебраических уравнений (СЛАУ) с помощью определителей удобно производить для систем 2-х или 3-х уравнений. Если же число уравнений больше, то гораздо выгоднее использовать метод Гаусса. Метод Гаусса заключается в последовательном исключении неизвестных.

Пусть необходимо решить систему:


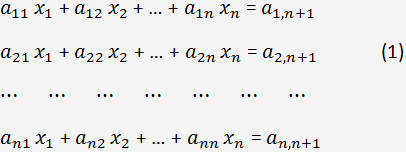
где x_i - неизвестные, i = 1, 2, ..., n; n < 200. Если число уравнений больше, то нужно применять итерационные методы решения.
a_i,j - элементы расширенной матрицы коэффициентов.

В соответствии с алгоритмом Гаусса выразим x₁ из первого уравнения
x₁ = (a_1,n+1 - a_1,2x₂ - ... - a_1nx_n)/a₁₁     (2)

Если a_1,1=0, то необходимо переставить уравнения системы. Затем подставим (2) во все уравнения системы (1), кроме первого. Таким образом, неизвестное x₁ будет исключено из всех уравнений системы, кроме первого.
При этом элементы расширенной матрицы преобразуются по формулам:

a_1j⁽¹⁾ = a_1j/a₁₁

a_ij⁽¹⁾ = a_ij - a_i1a_1j⁽¹⁾, i = 2,3,...,n; j = 1, 2, ..., n+1

В результате исключения x₁ из всех уравнений все элементы первого столбца преобразованной матрицы будут равны нулю, кроме a₁₁⁽¹⁾ = 1.

Аналогично, x₂ выражаем из 2-го уравнения и исключаем оставшихся уравнений системы и т.д.

В результате получаем преобразованную матрицу, у которой все элементы ниже главной диагонали равны нулю.

Выпишем соответствующие формулы для исключения неизвестного x_k и получения коэффициентов преобразованной матрицы.



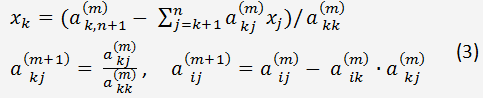
Теперь мы можем определить все неизвестные x_k последовательно, начиная с x_n и заканчивая x₁. Эта процедура называется обратным ходом метода Гаусса.

Для того, чтобы уменьшить погрешность при делении на диагональный элемент в формуле (3), рекомендуется осуществлять такую перестановку уравнений, чтобы поставить на диагональ наибольший по модулю из всех элементов рассматриваемого столбца. Модифицированный таким образом метод Гаусса называется методом Гаусса с выбором главного элемента.

Оценить погрешность численного решения системы можно с помощью вычисления невязок. Для этого численные решения x_k, k = 1, 2, ..., n, нужно подставить в систему и вычислить разность между правыми и левыми частями уравнений.


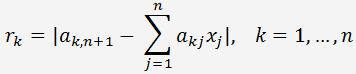
При малой погрешности решений величины невязок r_k будут равны нулю.