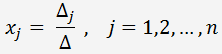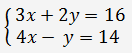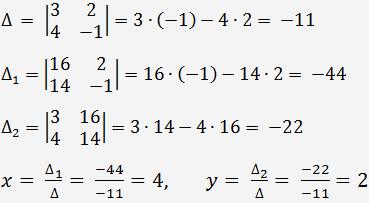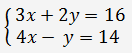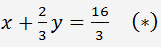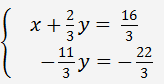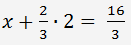Решение системы двух линейных уравнений с двумя неизвестными
Для решения системы двух уравнений с двумя неизвестными 2x2 с помощью калькулятора, введите коэффициенты системы и нажмите кнопку 'Решить'.
Решение систем линейных алгебраических уравнений
Система двух линейных уравнений с двумя неизвестными имеет следующий вид:
a
11x
1 + a
12x
2 = b
1
a
21x
1 + a
22x
2 = b
2
где x
1 и x
2 - неизвестные; a
11, a
12, a
21, a
22 - коэффициенты системы; b
1 и b
2 - свободные члены.
Так как в данной системе число уравнений равно числу неизвестных, то система называется квадратной.
Решение систем линейных уравнений (Правило Крамера)
Нахождние корней системы линейных уравнений по формулам Крамера удобно для систем из двух и трех уравнений, так как вычисление определителей четвертого и более высоких порядков является достаточно громоздкой процедурой. Правило Крамера подходит для решения квадратных систем линейных алгебраических уравнений, у которых определитель основной матрицы не равен нулю.
Рассмотрим систему n линейных уравнений с n неизвестными x
1, x
2, ..., x
n:
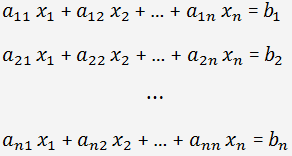
Матрица, составленная из коэффициентов этой системы, является квадратной, так как у нее n строк и n столбцов. Обозначим определитель этой матрицы:
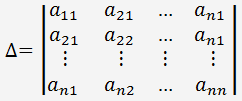
Через
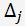
обозначим определитель матрицы системы, в которой j столбец заменен на столбец правых частей уравнений
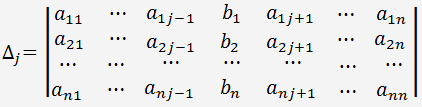
Тогда, если определитель
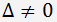
, то эта система совместна и имеет единственное решение, которое находится по формуле Крамера (правило Крамера):
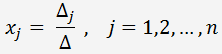
Рассмотрим применение формул Крамера на примере.
Пусть дана система двух линейных уравнений с двумя неизвестными
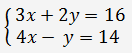
По формулам Крамера получаем
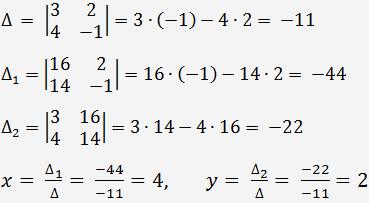
Решения систем линейных уравнений методом Гаусса
Метод Гаусса заключается в последовательном исключении неизвестных. С помощью простых преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно находятся все неизвестные, начиная с x
n и заканчивая x
1.
Пример решения системы двух линейных уравнений методом Гаусса
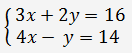
Разделим первое уравнение системы на 3
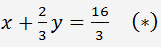
Умножим уравнение (*) на 4 и вычтем из второго уравнения. Получим следующую систему уравнений
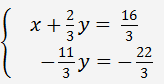
Из последнего уравнения находим y=2. Подставляя найденное значение в первое уравнение, находим x.
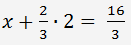
Ответ: x=4, y=2.

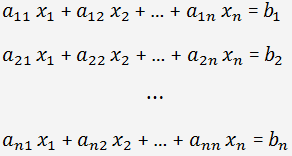
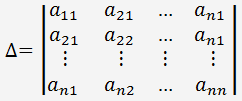
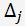 обозначим определитель матрицы системы, в которой j столбец заменен на столбец правых частей уравнений
обозначим определитель матрицы системы, в которой j столбец заменен на столбец правых частей уравнений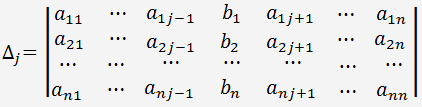
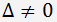 , то эта система совместна и имеет единственное решение, которое находится по формуле Крамера (правило Крамера):
, то эта система совместна и имеет единственное решение, которое находится по формуле Крамера (правило Крамера):