Операции с комплексными числами, представленными в алгебраической форме

Арифметические действия с комплексными числами аналогичны действиям с алгебраическими двучленами.

Сложение комплексных чисел

Чтобы сложить два комплексных числа, нужно сложить действительные числа их действительных и мнимых частей. Формула сложения двух комплексных чисел a+bi и c+di записывается так:

(a + bi) + (c + di) = a+c+(b+d)i.

Приведем формулу сложения для двух комплексных чисел (a;b) и (c;d), представленных в виде упорядоченных пар действительных чисел:

(a;b) + (c;d) = (a+c;b+d).

Сумма двух комплексно сопряженных чисел всегда равна действительному числу:

(a + bi) + (a - bi) = 2a.

Примеры.
1) (3+4i) + (2-4i) = 5;
2) (-2+i) + (1+3i) = -1+4i;
3) (-5+5i) + (5-3i) = 2i;
4) 6 + (-3-8i) = 3-8i.

Вычитание комплексных чисел

Вычитание комплексных чисел сводится к вычитанию действительных чисел их действительных и мнимых частей:

(a + bi) - (c + di) = a-c+(b-d)i.

Для двух комплексных чисел (a;b) и (c;d), представленных в виде упорядоченных пар действительных чисел, аналогичная формула записывается так:

(a;b) - (c;d) = (a-c;b-d).

Примеры.
1) (3+4i) - (2-4i) = 1+8i;
2) (-2+i) - (1+3i) = -3-2i;
3) (-5+5i) - (5-3i) = -10+8i;
4) 6 - (-3-8i) = 9+8i.

Умножение комплексных чисел

Умножение комплексных чисел осуществляется так же, как умножение алгебраических двучленов. Приведем вывод соответствующей формулы с учетом того, что i²= -1:

(a + bi)(c + di) = ac + adi + bci + bdi² = ac-bd + (ad+bc)i.

Для двух комплексных чисел (a;b) и (c;d), представленных в виде упорядоченных пар действительных чисел, аналогичная формула записывается так:

(a;b)(c;d) = (ac-bd;ad+bc).

Произведение двух сопряженных комплексных чисел a+bi и a-bi всегда является действительным числом, притом неотрицательным:

(a + bi)(a - bi) = a² - abi + abi - b²i² = a²+b².

Примеры.
1) (3+4i)(2-4i) = 6-12i+8i+16 = 22-4i;
2) (-2+i)(1+3i) = -2-6i+i-3 = -5-5i;
3) (-5+5i)(5-3i) = -25+15i+25i+15 = -10+40i;
4) 6(-3-8i) = -18-48i;
5) (3-2i)(3+2i) = 9+4 = 13.

Деление комплексных чисел

Деление комплексного числа z₁ = a+bi на комплексное число z₂ = c+di осуществляется с помощью умножения числителя и знаменателя дроби z₁/z₂ на комплексно сопряженное знаменателю число. В результате в знаменателе получается действительное положительное число, так как z₂≠0. Таким образом, нахождение частного z₁/z₂ сводится к умножению z₁ на сопряженное знаменателю комплексное число и к делению полученного произведения на положительное число. Получим формулу частного от деления z₁/z₂:

z₁/z₂

=

a+bi/c+di

=

(a+bi)(c-di)/(c+di)(c-di)

=

ac+bd/c²+d²

+

bc-ad/c²+d²

i.

Аналогичная формула для двух комплексных чисел (a;b) и (c;d), представленных в виде упорядоченных пар действительных чисел, записывается так:

(a;b)/(c;d)

= (

ac+bd/c²+d²

;

bc-ad/c²+d²

)

.

Приведенные формулы слишком громоздкие и трудно запоминаются. Поэтому для деления комплексных чисел рекомендуется пользоваться формулой
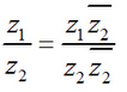
Примеры.
1)

Возведение комплексных чисел в степень с целым показателем

Возведение комплексных чисел в степень с целым показателем производится по тем же формулам и правилам, что и возведение в степень действительных чисел. Для любого комплексного числа z≠0 и целых m, n

z⁰ = 1;   z^-n = (1/z)ⁿ;   zⁿz^m=z^n+m;   zⁿ:z^m=z^n-m.

Примеры.
1) (3+2i)² = 9+12i-4 = 5+12i;
2) (2-5i)³ = 2³-3*2²*(5i)+3*2*(5i)²-(5i)³ = 8-60i-150+125i = -142+85i;
3) (1+i)⁴ = (1+i)²(1+i)² = (1+2i-1)(1+2i-1) = 2i*2i = -4;
4) (1+i)^-2 = 1/(1+i)² = 1/(1+2i-1) = 1*(-2i)/(2i*(-2i)) = -2i/4 = -(1/2)i.