Комплексные числа z, имеющие один и тот же модуль |z| = r, соответствуют, очевидно, точкам комплексной плоскости, расположенным на окружности с центром (0;0) и радиусом r. Если |z|≠0, то существует бесконечно много комплексных чисел с данным модулем. И существует только одно комплексное число z=0, которое имеет модуль, равный нулю.
Аргументы комплексного числа
Геометрически очевидно, что комплексное число z≠0, z=a+bi будет однозначно определено, если кроме модуля задать, например, величину угла φ между положительным направлением оси X и вектором z:
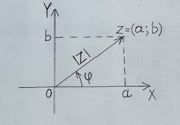
Аргументом комплексного числа z≠0 называется величина угла между положительным направлением оси X и вектором z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной,
если по часовой стрелке. Очевидно, аргумент комплексного числа определяется неоднозначно, так как любой угол, отличающийся на кратное 2π число, также будет аргументом числа z, то есть у каждого комплексного числа существует бесконечное множество аргументов.
Таким образом, задание модуля и аргумента однозначно определяет комплексное число. Для числа z=0 аргумент не определен, но только в этом случае число задается своим модулем. Аргумент комплексного числа, в отличие от модуля, определяется неоднозначно.
Действительная и мнимая части комплексного числа z=a+bi, как показывает рисунок, выражаются через его модуль r=|z| и аргумент φ следующим образом:
a=rcosφ; b=rsinφ.
Перепишем эту систему в виде:
cosφ=a/r; sinφ=b/r. ⇔ cosφ=a/√(a2+b2); sinφ=b/√(a2+b2).
Очевидно, решений φ этих уравнений бесконечное множество, так как любые два аргумента комплексного числа отличаются на число, кратное 2π. Все множество аргументов обозначается arg(z) или arg(a+bi). Если имеется в виду один конкретный аргумент, обычно его обозначают буквой φ.
Примеры нахождения аргументов комплексного числа
Пример 1.
Найти аргументы комплексного числа i.
Решение.
a+bi = i ⇔ a=0; b=1 ⇔ r=√(0+1)=1; cosφ = a/r = 0; sinφ = b/r = 1. Этим значениям косинуса и синуса соответствует значение аргумента φ=π/2.
⇔ r=1; φ=π/2.
Таким образом, arg(z) = π/2+2πk, где k - произвольное целое число.
Ответ: π/2+2πk, k∈Z.
Пример 2.
Найти аргументы комплексного числа -1+i.
Решение.
a+bi = -1+i ⇔ a=-1; b=1 ⇔ r=√(1+1)=√2; cosφ = a/r = -1/√2; sinφ = b/r = 1/√2 ⇔ r=√2; φ=3π/4.
Таким образом, arg(z) = 3π/4+2πk, где k - произвольное целое число.
Ответ: 3π/4+2πk, k∈Z.
Пример 3.
Найти аргументы комплексного числа -1-√3i.
Решение.
a+bi = -1-√3i ⇔ a=-1; b=-√3 ⇔ r=√(1+3)=2; cosφ = a/r = -1/2; sinφ = b/r = -√3/2 ⇔ r=2; φ=-2π/3.
Таким образом, arg(z) = -2π/3+2πk, где k - произвольное целое число.
Ответ: -2π/3+2πk, k∈Z.
Аргументы комплексного числа можно найти и другим способом. Из рисунка следует, что каждый из аргументов удовлетворяет уравнению:
tgφ=b/a.
Это уравнение имеет больше решений, чем система уравнений, которую мы использовали ранее. Но отбор нужных решений не представляет трудностей, так как из алгебраической формы записи комплексного числа сразу понятно, в каком квадранте комплексной плоскости число расположено.
Пример 4.
Найти аргументы комплексного числа -√3+i.
Решение.
a+bi = -√3+i ⇔ a=-√3; b=1 => tgφ = b/a = -1/√3 => φ=-π/6.
Но так как число z=-√3+i расположено во втором квадранте комплексной плоскости, то его аргументами будут числа φ=5π/6+2πk, k∈Z.
Ответ: 5π/6+2πk, k∈Z.
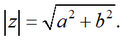 Очевидно, что сопряженные комплексные числа имеют равные модули и для них справедливо соотношение:
Очевидно, что сопряженные комплексные числа имеют равные модули и для них справедливо соотношение:
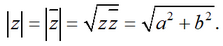 Для действительного числа z = a + 0*i модуль совпадает с абсолютной величиной числа a.
Для действительного числа z = a + 0*i модуль совпадает с абсолютной величиной числа a. Аргументом комплексного числа z≠0 называется величина угла между положительным направлением оси X и вектором z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной,
если по часовой стрелке. Очевидно, аргумент комплексного числа определяется неоднозначно, так как любой угол, отличающийся на кратное 2π число, также будет аргументом числа z, то есть у каждого комплексного числа существует бесконечное множество аргументов.
Аргументом комплексного числа z≠0 называется величина угла между положительным направлением оси X и вектором z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной,
если по часовой стрелке. Очевидно, аргумент комплексного числа определяется неоднозначно, так как любой угол, отличающийся на кратное 2π число, также будет аргументом числа z, то есть у каждого комплексного числа существует бесконечное множество аргументов.