Как известно, корень n-ой степени из комплексного числа
z,
z = r *(cosφ + isinφ)
имеет n комплексных значений
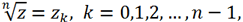
где
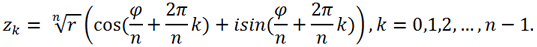
Следовательно,
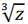
имеет три значения z
1, z
2, z
3, где
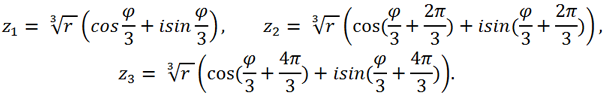
В формуле Кардано два кубических корня, и их значения нужно сочетать по следующему правилу: для каждого из трех значений первого кубического корня
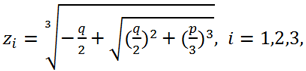
, берется такое значение второго кубического корня,
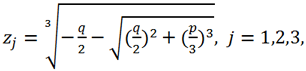
, чтобы выполнялось соотношение z
i*z
j = -
.
Чтобы избежать такого сочетания значений разных кубических корней, можно использовать формулу
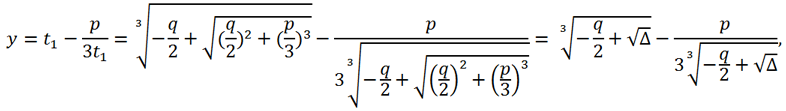
или, что то же самое,
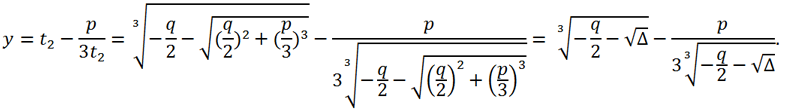
Каждому найденному по формуле Кардано значению y соответствует решение исходного уравнения x = y -
.
В зависимости от значения дискриминанта Δ кубическое уравнение может иметь либо 3 действительных корня (Δ <0), либо 1 действительный корень и два комплексно сопряженных (Δ > 0), либо 2 действительных корня (Δ=0) или один действительный корень (Δ=0, p=q=0). Рассмотрим все эти случаи.
1) Δ <0 => 3 действительных корня:
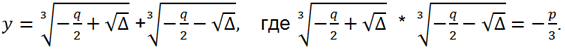
Если опустить промежуточные вычисления, то окончательные формулы для трех действительных корней канонического уравнения можно представить в виде
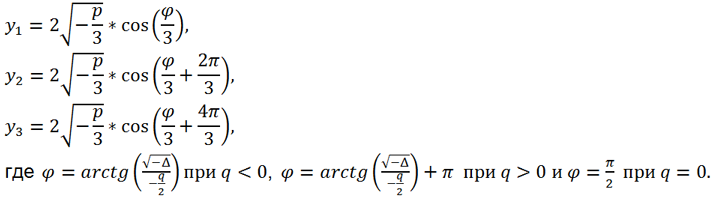
Тогда формулы для корней исходного уравнения будут иметь вид:
x
1 = y
1 -
, x
2 = y
2 -
, x
3 = y
3 -
.
2 ) Δ > 0 => 1 действительный корень и два комплексно сопряженных:
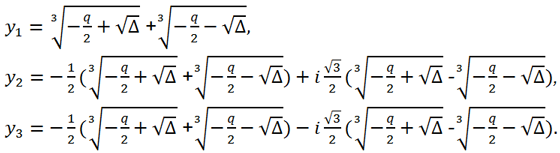
Формулы для корней исходного уравнения такие же, как в предыдущем случае
x
1 = y
1 -
, x
2 = y
2 -
, x
3 = y
3 -
.
3 ) Δ=0 => 2 действительных корня:
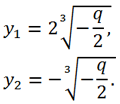
Следовательно, x
1 = y
1 -
, x
2 = y
2 -
.
Если Δ=0 и p=q=0, то у канонического уравнения только один корень y
1=0. Соответственно, исходное уравнение будет иметь единственный корень x = -
.
Если кубическое уравнение имеет целый или рациональный корень, то, конечно, проще всего найти этот корень подбором, затем делением свести исходное уравнение к квадратному. Если же рациональных корней нет, то только формула Кардано может помочь найти решение.
Практическое использование формулы Кардано для решения кубических уравнений крайне затруднительно из-за громоздких вычислений. Но в особых случаях, это сделать довольно просто, например, для первого случая (Δ < 0) при q = 0 для нахождения трех действительных корней, или для третьего случая (Δ = 0). Для второго случая, когда Δ > 0 , формулы для корней кубического уравнения можно выписать всегда. Таким образом, применение формулы Кардано оправдано, если уравнение не имеет рациональных корней.
Рассмотрим применение формулы Кардано для решения кубических уравнений на примерах.
Примеры.
Пример 1. Решить уравнение x
3 + 6x
2 + 3x - 10 = 0.
Решение.
Данное уравнение легко решается и без применения формулы Кардано. Легко подобрать корень x = 1. Делением на x - 1 левой части уравнения по схеме Горнера получаем
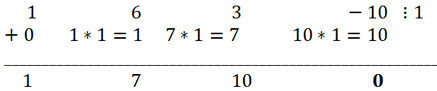
Следовательно, x
2 + 7x + 10 = 0. Решая это квадратное уравнение, получаем
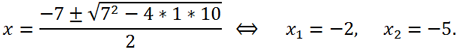
А теперь найдем корни исходного уравнения по формуле Кардано. Для данного уравнения a = 1, b = 6, c =3, d = -10. Замена переменной x = y -
b/3a
= y -
приводит исходное уравнение к виду y
3 + py + q = 0, где
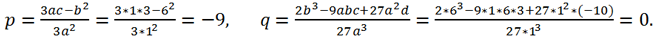
Вычислим дискриминант этого уравнения
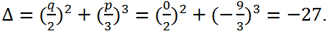
Так как Δ <0 => каноническое уравнение имеет 3 действительных корня. Поскольку q = 0 => φ =
=>
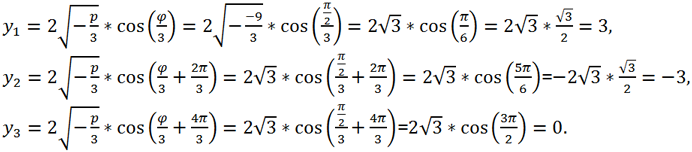
Тогда для корней исходного уравнения получаем:
x
1 = y
1 - 2 = 3 - 2 = 1,
x
2 = y
2 - 2 = -3 - 2 = -5,
x
3 = y
3 - 2 = 0 - 2 = -2.
Ответ: -5, -2, 1.
Пример 2. Решить уравнение x
3 + 3x
2 + 4x + 2 = 0.
Решение.
Для данного уравнения a = 1, b = 3, c =4, d = 2. Замена переменной x = y -
приводит исходное уравнение к виду y
3 + py + q = 0, где
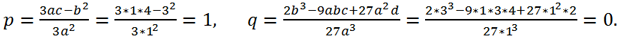
Вычислим дискриминант этого уравнения
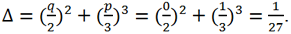
Так как Δ >0 => каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:
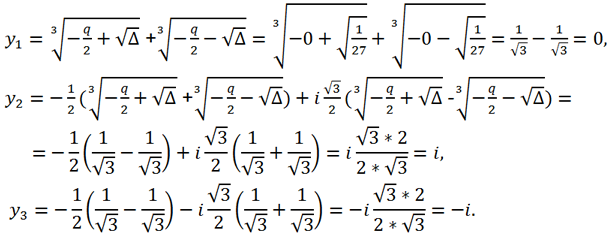
Тогда для корней исходного уравнения получаем:
x
1 = y
1 - 1 = 0 - 2 = -1,
x
2 = y
2 - 1 = i - 1 = i - 1,
x
3 = y
3 - 1 = -i - 1 = -i - 1.
Ответ: -1, -1+i, -1-i.
Пример 3. Решить уравнение x
3 + 12x
2 + 36x + 32 = 0.
Решение.
Для данного уравнения a = 1, b = 12, c =36, d = 32. Замена переменной x = y -
приводит исходное уравнение к виду y
3 + py + q = 0, где
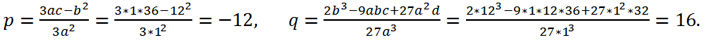
Вычислим дискриминант этого уравнения
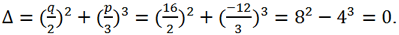
Так как Δ = 0 => уравнение имеет 2 действительных корня:
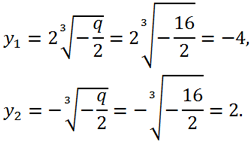
Тогда для корней исходного уравнения получаем:
x
1 = y
1 - 4 = -4 - 4 = -8,
x
2 = y
2 - 4 = 2 - 4 = -2.
Ответ: -8, -2.
Пример 4. Решить уравнение x
3 + 9x
2 + 9x - 137 = 0.
Решение.
Для данного уравнения a = 1, b = 9, c =9, d = -137. Замена переменной x = y -
приводит исходное уравнение к виду y
3 + py + q = 0, где
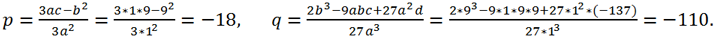
Вычислим дискриминант этого уравнения
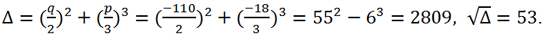
Так как Δ >0 => каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:
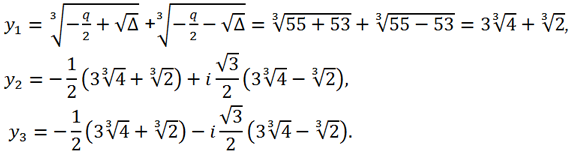
Тогда для корней исходного уравнения получаем:
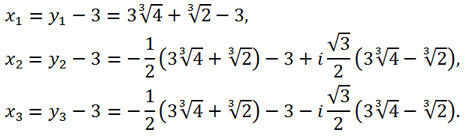
Ответ:
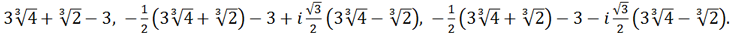 Пример 5.
Пример 5. Решить уравнение x
3 + 18x
2 + 90x + 50 = 0.
Решение.
Для данного уравнения a = 1, b = 18, c =90, d = 50. Замена переменной x = y -
приводит исходное уравнение к виду y
3 + py + q = 0, где
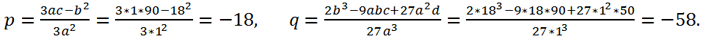
Вычислим дискриминант этого уравнения
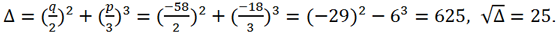
Так как Δ > 0 => каноническое уравнение имеет 1 действительный корень и два комплексно сопряженных:
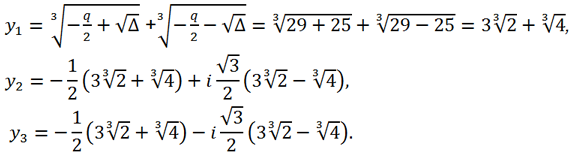
Тогда для корней исходного уравнения получаем:
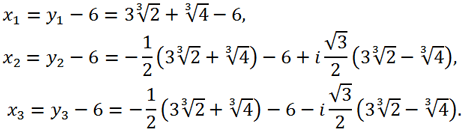
Ответ:
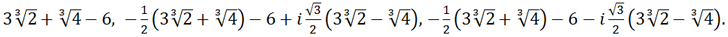
Так как запомнить промежуточные формулы для нахождения корней кубического уравнения с помощью формулы Кардано довольно сложно, то можно просто повторить вывод формулы Кардано для данного уравнения. Рассмотрим соответствующий пример.
Пример. Найти действительные корни уравнения x
3 + 12x
2 + 3x + 4 = 0.
Решение.
Для данного уравнения a = 1, b = 12, c = 3, d = 4. Сделаем замену переменной x = y -
:
(y - 4)
3 + 12(y - 4)
2 + 3(y - 4) + 4 = 0 <=>
<=> y
3 - 12y
2 + 48y - 64 + 12y
2 - 96y + 192 + 3y - 8 = 0 <=>
<=> y
3 - 45y + 120 = 0.
Следовательно, p = -45, q = 120, Δ = (60)
2 - (15)
3 = 225 >0. Значит, исходное уравнение имеет один действительный корень.
Теперь сделаем следующую замену переменной
y = t -
p/3t
= t +
45/3t
= t +
15/t
. Получим
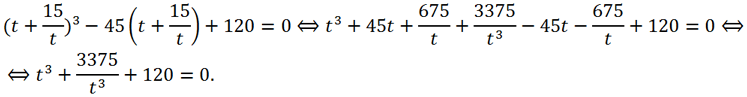
Это уравнение домножим на t
3 и получим квадратное уравнение относительно t
3:
t
6 + 120t
3 + 3375 = 0.
Следовательно,
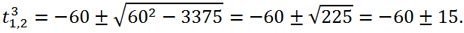
Тогда
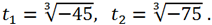
Теперь можно найти y по формуле y = t +
.
Вместо t можно подставить или
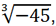
, или
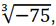
, результат будет один и тот же:
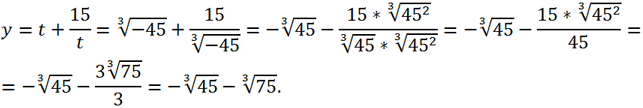
Или
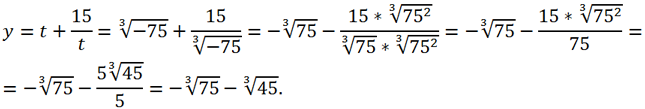
Таким образом, действительный корень исходного уравнения равен
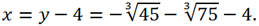
Ответ:
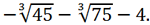
.
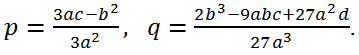
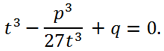
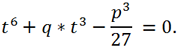
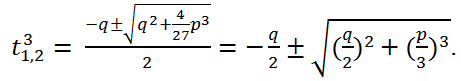
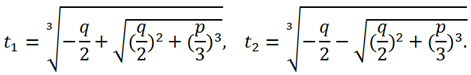
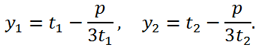
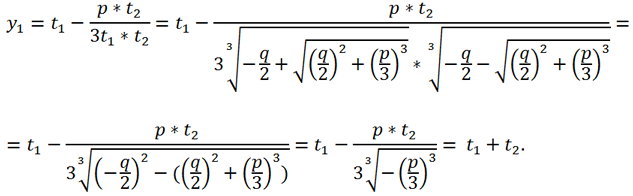
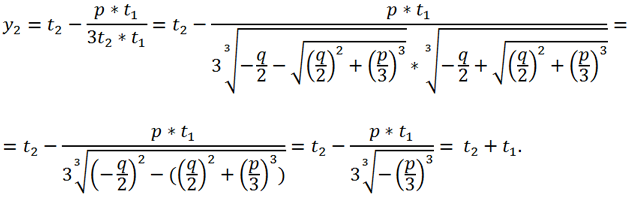
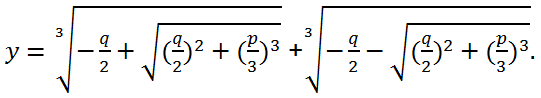
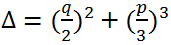 называется дискриминантом кубического уравнения y3 + py + q = 0.
называется дискриминантом кубического уравнения y3 + py + q = 0.
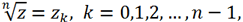
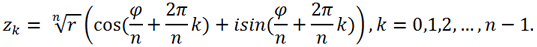
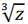 имеет три значения z1, z2, z3, где
имеет три значения z1, z2, z3, где 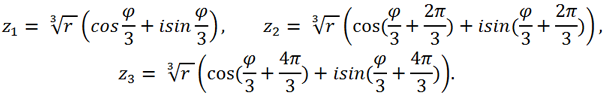
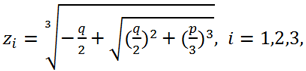 , берется такое значение второго кубического корня,
, берется такое значение второго кубического корня, 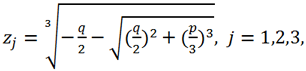 , чтобы выполнялось соотношение zi*zj = -
, чтобы выполнялось соотношение zi*zj = -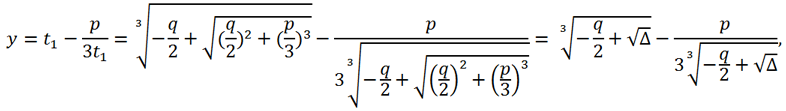
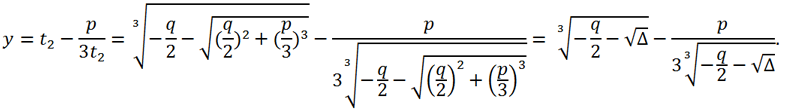
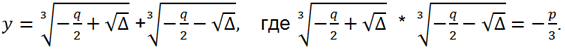
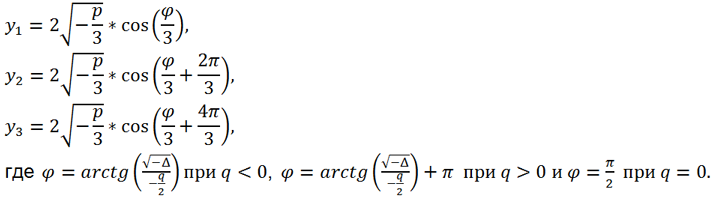
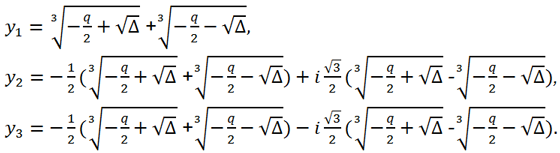
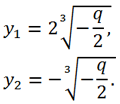
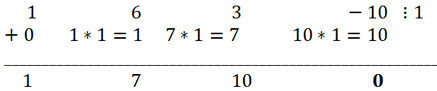
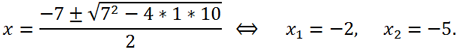
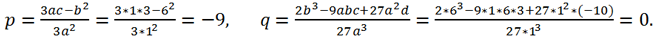
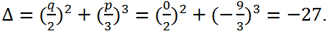
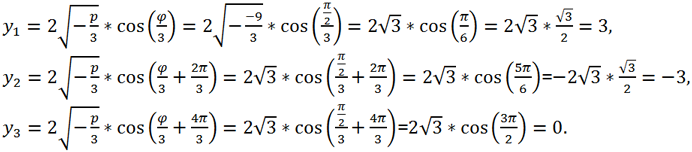
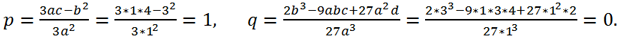
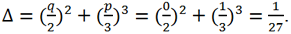
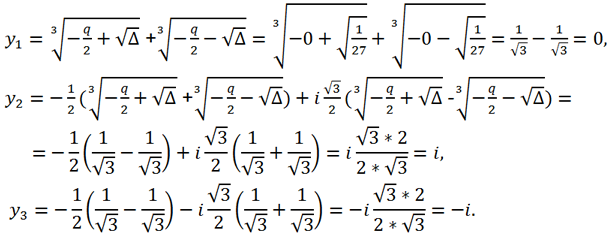
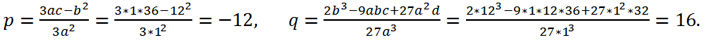
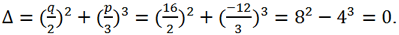
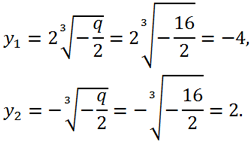
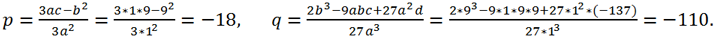
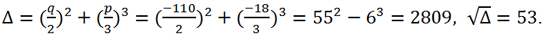
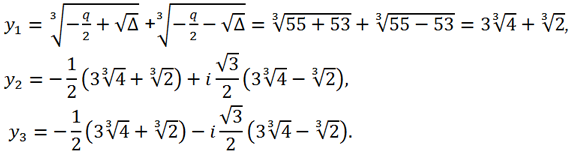
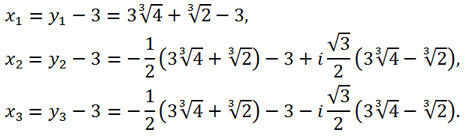
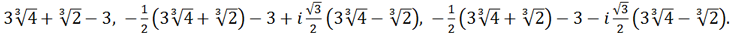
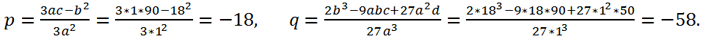
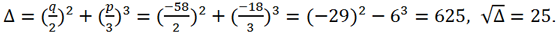
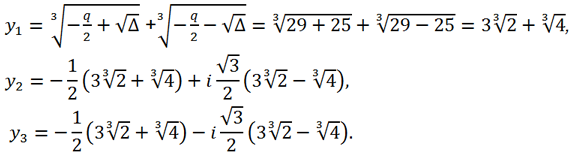
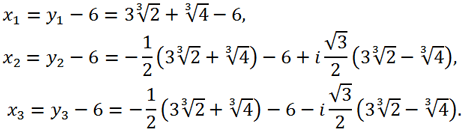
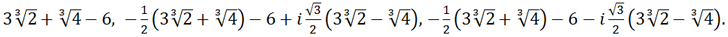
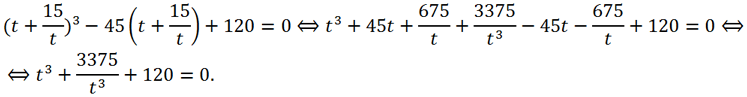
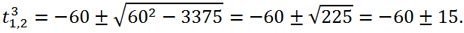
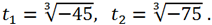 Теперь можно найти y по формуле y = t +
Теперь можно найти y по формуле y = t + 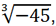 , или
, или 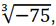 , результат будет один и тот же:
, результат будет один и тот же: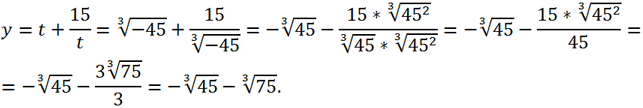
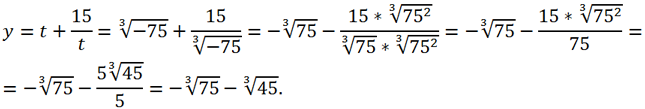
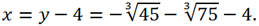
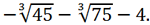 .
.