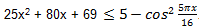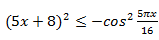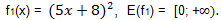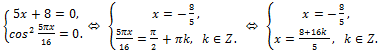Метод решения комбинированных уравнений и неравенств, основанный на анализе областей значений их левых и правых частей.
Рассмотрим способ решения нестандартных уравнений и неравенств, при котором сравниваются области значений двух функций, представляющих левую и правую части уравнения или неравенства. Суть метода в том, что область значений одной функции имеет только одну общую точку с областью значений второй функции. Следовательно, исходное уравнение или неравенство имеет решение только в том случае, когда левая и правая части уравнения равны этому значению.
Примеры решений комбинированных уравнений и неравенств.
Пример 1.
Решить уравнение cos(x) = x
2 -2x + 2.
Решение.
1) Левая часть уравнения f
1(x) = cos(x). Область значений функции E(f
1) = [-1; 1].
2) Правая часть уравнения f
2(x) = x
2 -2x + 2 представляет собой параболу с ветвями, направленными вверх. Найдем координаты вершины:
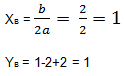
Следовательно,
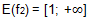
3) Решение уравнения возможно только, если

Но
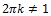
для любых
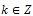
Следовательно, корней нет.
Ответ: корней нет.
Пример 2.
Решить уравнение
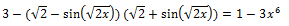 Решение.
Решение.
ОДЗ:
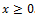
С помощью элементарных преобразований приведем уравнение к виду:
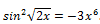
1)
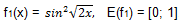
2)

3)
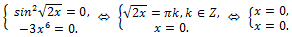 Ответ:
Ответ: x = 0.
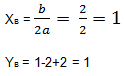
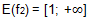
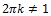 для любых
для любых 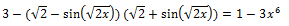
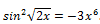
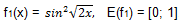

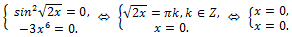
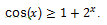 Решение.
Решение.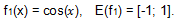
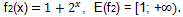
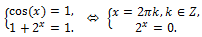
 Решение.
Решение.