language  RU
  ☰
Скачать
Продукты
Математика

Метод Феррари для решения уравнений четвертой степени

Алгебраическое уравнение четвертой степени в общем случае имеет вид a0x4 + a1x3 + a2x2 + a3x + a4 = 0,
коэффициенты ai – действительные (или комплексные) числа, причем a0 ≠ 0. Не нарушая общности, будем рассматривать уравнения 4 степени в виде x4 + ax3 + bx2 + cx + d = 0 (так как a0 ≠ 0, просто разделим на a0 левую и правую части уравнения).
Наиболее простой метод решения этого уравнения предложен Л. Феррари. Идея метода Феррари состоит в том, чтобы представить левую часть уравнения в виде разности квадратов двух многочленов. Тогда эту разность можно разложить на два квадратичных множителя, и решение исходного уравнения сведется к решению двух квадратных уравнений.
Введем вспомогательную переменную t и представим левую часть уравнения в виде
(x2 + (a/2)x + t/2)2 - a2x2/4 - atx/2 - t2/4 - tx2 + bx2 + cx + d =
 = (x2 + (a/2)x + t/2)2 - [(a2/4 + t - b)x2 + (at/2 - c)x + t2/4 - d].
Наша цель - подобрать такое значение вспомогательной переменной t, чтобы выражение в квадратных скобках было полным квадратом. Для этого необходимо и достаточно, чтобы дискриминант квадратного трехчлена в квадратных скобках равнялся нулю, то есть
D = (at/2 - c)2 - 4(a2/4 + t - b)(t2/4 - d) = 0.
После раскрытия скобок получим следующее кубическое уравнение
t3 - bt2 + (ac-4d)t - (c2 + a2d - 4bd) = 0.
Пусть t0 - произвольный корень этого уравнения. Его можно найти либо по формуле Кардано, либо любым другим способом. Итак, при t=t0 многочлен в квадратных скобках представляет собой полный квадрат, то есть имеет один двухкратный корень x0
x0 = -(at0/2 - c) / (2(a2/4 + t0 - b)).
Следовательно,
(a2/4 + t0 - b)x2 + (at0/2 - c)x + t02/4 - d = (a2/4 + t0 - b)(x - x0)2 = (gx + h)2
при некоторых значениях коэффициентов g, h. Таким образом, для исходного уравнения справедливо
(x2 + (a/2)x + t0/2)2 - (gx + h)2 = 0 <=>
<=> (x2 + (a/2)x + t0/2 - gx - h)(x2 + (a/2)x + t0/2 + gx + h)<=>
<=> x2 + (a/2-g)x + t0/2 - h = 0 или x2 + (a/2+g)x + t0/2 + h = 0.
Решив эти квадратные уравнения, найдем 4 корня исходного уравнения.

Калькуляторы для решения примеров и задач по математике

 Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее ...

Приведем одно полезное равенство. Пусть x1, x2 - корни первого квадратного уравнения, а x3, x4 - корни второго. Тогда по теореме Виета
x1x2 = t0/2 - h,   x3x4 = t0/2 + h.
Сложив эти два равенства, получим выражение для вспомогательной переменной t0 через корни исходного уравнения:
t0 = x1x2 + x3x4.
Рассмотрим на примерах решения уравнений 4 порядка методом Феррари.

Примеры решения уравнений четвертого порядка методом Феррари


Пример 1.
Решить уравнение x4 + 2x3 - 6x2 - 5x + 2 = 0.
Решение.
Для исходного уравнения a=2, b=-6, c=-5, d=2. Выделим полный квадрат в левой части уравнения
x4 + 2x3 - 6x2 - 5x + 2 = (x2 + x + t/2)2 - x2 - tx - t2/4 - tx2 - 6x2 - 5x + 2 =  (x2 + x + t/2)2 - [(t+7)x2 + (t+5)x + t2/4 - 2].
Приравняем к нулю дискриминант выражения в квадратных скобках D = (t+5)2- 4(t+7)(t2/4 - 2) = 0.
После раскрытия скобок получаем t3 + 6t2 - 18t - 81 = 0. Целочисленные решения этого уравнения надо искать среди делителей свободного члена -81: ±1, ±3,... . Непосредственной подстановкой убеждаемся, что t = -3 является решением кубического уравнения. Следовательно, многочлен в квадратных скобках при t=-3 представляет собой полный квадрат:
4x2 + 2x + 1/4 = (2x+1/2)2.
Таким образом, получаем
x4 + 2x3 - 6x2 - 5x + 2 = 0 <=>(2x+1/2)2 = 0.
Раскладывая на множители последнее уравнение и приравнивая множители к нулю, получим два квадратных уравнения
x2 - x - 2 = 0   или   x2 + 3x - 1 = 0.
Решения этих квадратных уравнений дадут нам 4 действительных корня исходного уравнения:
x1 = -1, x2 = 2, x3,4 = (-3±√13)/2.
Ответ: (-3-√13)/2, -1, (-3+√13)/2, 2.

Пример 2.
Решить уравнение x4 - 2x3 + 4x2 - 2x + 3 = 0.
Решение.
Для исходного уравнения a=-2, b=4, c=-2, d=3. Выделим полный квадрат в левой части уравнения
x4 - 2x3 + 4x2 - 2x + 3 = (x2 - x + t/2)2 - x2 + tx - t2/4 + tx2 + 4x2 - 2x + 3 =  (x2 - x + t/2)2 - [(t-3)x2 + (-t+2)x + t2/4 - 3].
Приравняем к нулю дискриминант выражения в квадратных скобках D = (-t+2)2 - 4(t-3)(t2/4 - 3) = 0.
После раскрытия скобок получаем t3 - 4t2 - 8t + 32 = 0. Целочисленные решения этого уравнения надо искать среди делителей свободного члена 32: ±1, ±2, ±4,... . Легко видеть, что t0 = 4 является решением кубического уравнения. Следовательно, многочлен в квадратных скобках при t=4 представляет собой полный квадрат:
x2 - 2x + 1 = (x - 1)2.
Таким образом, получаем
x4 - 2x3 + 4x2 - 2x + 3 = 0 <=> (x2 - x + 2)2 - (x-1)2 = 0 <=> (x2 - 2x + 3)(x2 + 1) = 0.
Приравнивая множители к нулю, получим два квадратных уравнения
x2 - 2x + 3 = 0   или   x2 + 1 = 0.
Решения этих квадратных уравнений дадут нам 4 комплексных корня исходного уравнения:
x1,2 = 1±i√2,    x3,4 = ±i.
Ответ: 1-i√2, 1+i√2, -i, i.

Пример 3.
Решить уравнение x4 - 2x3 - 10x2 + 24x - 24 = 0.
Решение.
Для исходного уравнения a=-2, b=-10, c=24, d=-24. Выделим полный квадрат в левой части уравнения
x4 - 2x3 - 10x2 + 24x - 24 = (x2 - x + t/2)2 - x2 + tx - t2/4 - tx2 - 10x2 + 24x - 24 =  (x2 - x + t/2)2 - [(t+11)x2 - (t+24)x + t2/4 + 24].
Приравняем к нулю дискриминант выражения в квадратных скобках D = (t+24)2- 4(t+11)(t2/4 + 24) = 0.
После раскрытия скобок получаем t3 + 10t2 + 48t + 480 = 0. Легко убедиться простой подстановкой, что t = -10 является решением кубического уравнения. Следовательно, многочлен в квадратных скобках при t=-10 представляет собой полный квадрат:
x2 - 14x + 49 = (x - 7)2.
Таким образом, получаем
x4 - 2x3 - 10x2 + 24x - 24 = 0 <=> (x2 - x - 5)2 - (x-7)2 = 0 <=> (x2 - 2x + 2)(x2 - 12) = 0.
Приравнивая множители к нулю, получим два квадратных уравнения
x2 - 2x + 2 = 0   или   x2 - 12 = 0.
Решения этих квадратных уравнений дадут нам 4 корня исходного уравнения: 2 комплексных и 2 дейстительных.
x1,2 = 1±i,    x3,4 = ±2√3.
Ответ: 1-i, 1+i, -2√3, 2√3.

Пример 4.
Решить уравнение x4 + 4x - 1 = 0.
Решение.
Для исходного уравнения a=0, b=0, c=4, d=-1. Выделим полный квадрат в левой части уравнения
x4 + 4x - 1 = (x2 + t/2)2 - x2t - t2/4 + 4x - 1 =  (x2 + t/2)2 - [tx2 - 4x + t2/4 + 1].
Приравняем к нулю дискриминант выражения в квадратных скобках D = 42- 4t(t2/4 + 1) = 0.
После раскрытия скобок и деления на 4 обеих частей равенства получаем t3 + 4t -16 = 0. Целочисленные решения этого уравнения надо искать среди делителей свободного члена -16. Непосредственной подстановкой убеждаемся, что t = 2 является решением кубического уравнения. Следовательно, многочлен в квадратных скобках при t=2 представляет собой полный квадрат:
2x2 - 4x + 2 = (√2x-√2)2.
Таким образом, получаем
x4 + 4x - 1 = 0 <=> (x2 + 1)2 - (√2x-√2)2 = 0  <=> (x2 - √2x + 1 + √2)(x2 + √2x + 1 - √2) = 0.
Приравнивая множители к нулю, получим два квадратных уравнения
x2 - √2x + 1 + √2 = 0   или   x2 + √2x + 1 - √2 = 0.
Решения этих квадратных уравнений дадут нам 4 корня исходного уравнения: 2 комплексных и 2 дейстительных.
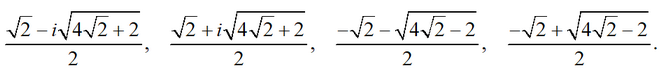
Пример 4 - корни уравнения 4 порядка Ответ:Пример 4 - корни уравнения 4 порядка
RNG - Random Number Generator app
Продукты
Техподдержка
четверг, 3 апреля, 2025

О компании
Контакты
Политика конфиденциальности
Условия предоставления услуг


language Русский
Copyright © 2025 Intemodino Group s.r.o.
Все права защищены