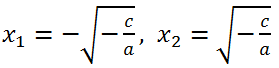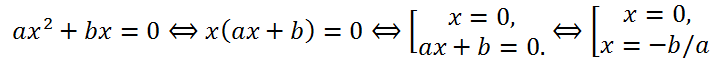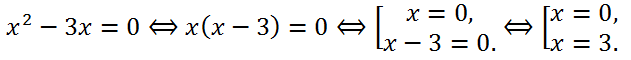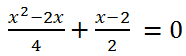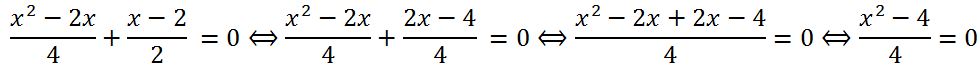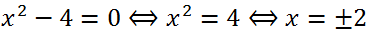Корни неполного квадратного уравнения
1. Если квадратное уравнение имеет вид
ax2 = 0, то оно имеет единственный корень x = 0.
2. Если квадратное уравнение имеет вид
ax2 + с = 0, то
ax2 = -с и, следовательно,
.
Правая часть последнего уравнения – число, не равное нулю по условию. Следовательно, если правая часть меньше нуля, то уравнение
, а значит, и исходное
ax2 + с = 0, корней не имеет.
Если же правая часть больше нуля, то уравнение
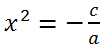
имеет два корня
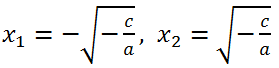
3. Если квадратное уравнение имеет вид ax
2 + bx = 0, то используя метод разложения на множители, получим
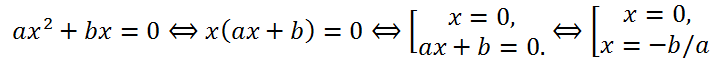
Таким образом, исходное уравнение имеет два корня x
1=0 и x
2 = -
.
Примеры решения неполных квадратных уравнений
Пример 1.
Решить квадратное уравнение x
2 - 3x = 0.
Решение.
Уравнение x
2 - 3x = 0 неполное квадратное, поэтому будем решать его методом разложения на множители:
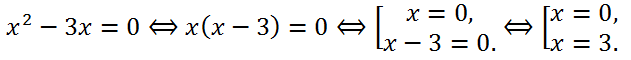 Ответ:
Ответ: 0, 3.
Пример 2.
Решить уравнение
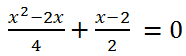 Решение.
Решение.
Приведем к общему знаменателю левую часть уравнения:
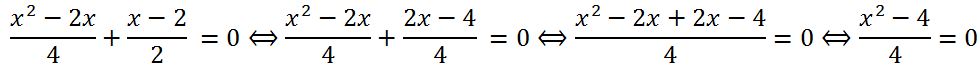
Умножим на 4 обе части уравнения:
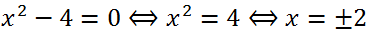 Ответ:
Ответ: -2, 2.
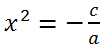 имеет два корня
имеет два корня