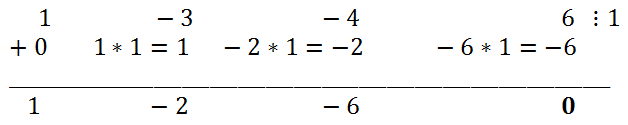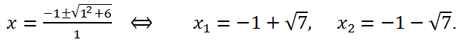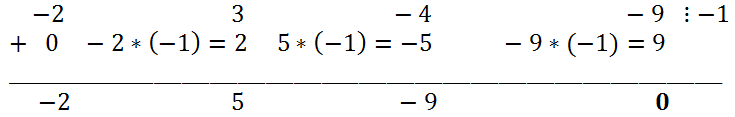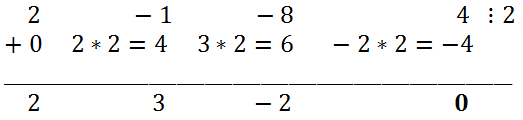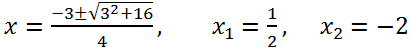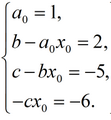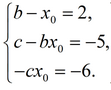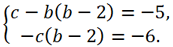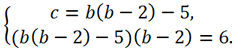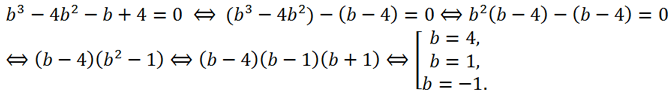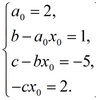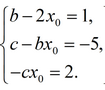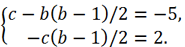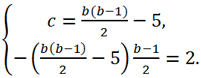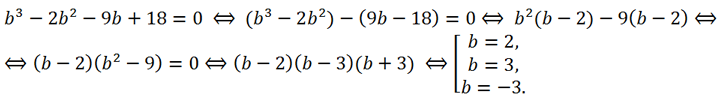Решение кубических уравнений методом разложения на множители

Согласно основной теореме алгебры, кубическое уравнение всегда имеет 3 корня (с учётом кратности), причем по крайней мере один из корней - вещественный, так как если корнем является комплексное число, то и комплексно сопряженное тоже будет его корнем. Таким образом, кубический многочлен a(x) = a₀*x³ + a₁*x² + a₂*x + a₃, a₀ ≠ 0, всегда можно разложить на два множителя, один из которых линейный, а второй квадратичный: a(x) = (x - x₀) (a₀x² + bx + c). В свою очередь многочлен второй степени a₀x² + bx + c может иметь 2 различных действительных корня, 1 действительный корень или 2 комплексно сопряженных корня.
Соответственно, получаем такие случаи разложения на множители многочлена a(x):

1) a(x) = a₀ (x - x₀) (x - x₁) (x - x₂)
2) a(x) = a₀ (x - x₀) (x - x₁)²
3) a(x) = a₀ (x - x₀)³
4) a(x) = (x - x₀) (a₀x² + bx + c), если b² - 4a₀c < 0.
Таким образом, приравнивая каждый множитель в разложении к нулю, найдем все корни кубического уравнения в каждом случае. Рассмотрим решение кубических уравнений методом разложения на множители на примерах.

Примеры решения кубических уравнений методом разложения на множители

Пример 1.
Решить уравнение x³ - 3x² - 4x + 6 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±2, ±3, ±6. Значит, корни уравнения нужно искать среди них. Простой подстановкой убеждаемся, что корнем уравнения является число 1. Следовательно, исходное уравнение эквивалентно (x - 1)*(a₀x² + bx + c) = 0.
Чтобы найти многочлен a₀x² + bx + c, нужно левую часть исходного уравнения разделить на x-1. Для деления многочлена на двучлен будем использовать схему Горнера.



Таким образом, x³ - 3x² - 4x + 6 = (x - 1)(x² - 2x - 6). Следовательно, исходное уравнение эквивалентно (x - 1) (x² - 2x - 6) = 0.
Осталось решить квадратное уравнение x² - 2x - 6 = 0.


Ответ: -1- √7, 1 ,-1+√7.

Пример 2.
Найти действительные корни уравнения -2x³ + 3x² - 4x - 9 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±3, ±9. Делителями старшего коэффициента являются числа: ±1, ±2. Значит, корни исходного уравнения могут быть среди чисел: ±1, ±3, ±9, .
Снова простой подстановкой убеждаемся, что -1 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x + 1.


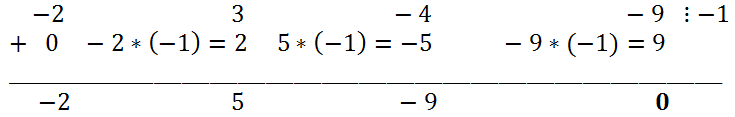
Таким образом, -2x³ + 3x² - 4x - 9 = (x + 1)(-2x² + 5x - 9). Следовательно, исходное уравнение эквивалентно (x + 1) (-2x² + 5x - 9)=0. Решая квадратное уравнение -2x² + 5x - 9 = 0, получаем, что его дискриминант < 0, следовательно, действительных корней у него нет.
Ответ: -1.

Пример 3. Решить уравнение 2x³ - x² - 8x + 4 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±2, ±4. Делителями старшего коэффициента являются числа: ±1, ±2.
Значит, корни исходного уравнения могут быть среди чисел: ±1, ±2, ±4.
Простой подстановкой убеждаемся, что 2 является корнем уравнения. С помощью схемы Горнера делим левую часть исходного уравнения на x - 2.


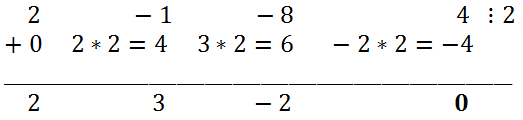
Таким образом, 2x³ - x² - 8x + 4 = (x - 2)(2x² + 3x - 2). Следовательно, исходное уравнение эквивалентно (x - 2) (2x² + 3x - 2) = 0. Решая квадратное уравнение 2x² + 3x - 2 = 0, получаем,


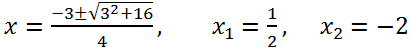Ответ: -2, , 2.

Еще один способ разложения на множители многочлена третьей степени - метод неопределенных коэффициентов. Он довольно громоздкий, но иногда бывает очень полезным при решении разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x₀)*(a₀x² + bx + c). Раскрывая скобки, получим a(x) = a₀x³ + x²(b - a₀x₀) + x*(c - bx₀) - cx₀. Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a₀, b, c и x₀. Рассмотрим применение метода неопределенных коэффициентов на примерах.

Пример 4.
Решить уравнение x³ + 2x² - 5x - 6 = 0.
Решение.
Так как любой многочлен 3 степени можно представить в виде a₀x³ + x²(b - a₀x₀) + x*(c - bx₀) - cx₀, то приравнивая коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:


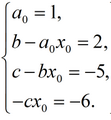
Или
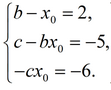
Выразим из первого уравнения x₀ = b - 2 и подставим в два оставшихся. Получим


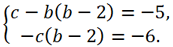
Теперь выразим переменную c из первого уравнения и подставим во второе.


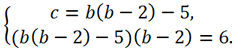
Раскрывая скобки во втором уравнении и решая его, находим b:


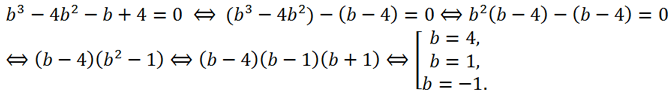
Если b=4, то c=3, x₀ = 2. Следовательно, x³ + 2x² - 5x - 6 = (x - 2)(x² - 4x + 3)=(x - 2)(x + 1)(x + 3).
Если b = 1, то c = -6, x₀ = -1. Следовательно, x³ + 2x² - 5x - 6 = (x + 1)(x² + x - 6)=(x + 1)(x + 3)(x - 2).
Если b = -1, то c = -2, x₀ = -3. Следовательно, x³ + 2x² - 5x - 6=(x + 3)(x² - x - 2) = (x + 3)(x - 2)(x + 1).
Таким образом, исходное уравнение эквивалентно уравнению (x + 3)(x - 2)(x + 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -3, x = 2, x = -1.
Ответ: -3, -1, 2.

Пример 5.
Решить уравнение 2x³ + x² - 5x + 2 = 0.
Решение.
Приравнивая соответствующие коэффициенты при одинаковых степенях x, получаем следующую систему уравнений:


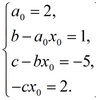
Или
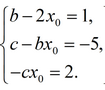
Выразим из первого уравнения x₀ =  и подставим в два оставшихся. Получим

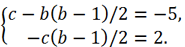
Теперь из первого уравнения выразим переменную c и подставим во второе.


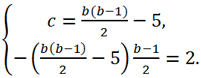
Умножая левую и правую части второго уравнения на 4 и раскрывая скобки, находим b:


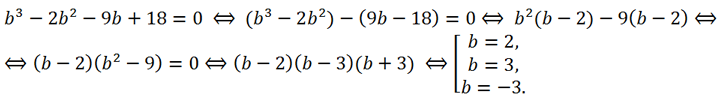
Если b=2, то c=-4, x₀ = . Следовательно, 2x³ + x² - 5x + 2 = (x - )(2x² + 2x - 4) = 2(x - )(x - 1)(x + 2).
Если b = 3, то c = -2, x₀ = 1. Следовательно, 2x³ + x² - 5x + 2 = (x - 1)(2x² + 3x - 2)=2(x - 1)(x - )(x + 2).
Если b = -3, то c = 1, x₀ = -2. Следовательно, 2x³ + x² - 5x + 2 = (x + 2)(2x² - 3x + 1) = 2(x + 2)(x - )(x - 1).
Следовательно, исходное уравнение эквивалентно уравнению 2(x + 2)(x - )(x - 1) = 0.
Приравнивая к нулю каждый из множителей, получаем корни уравнения x = -2, x = , x = 1.
Ответ: -2, , 1.