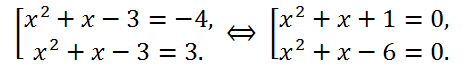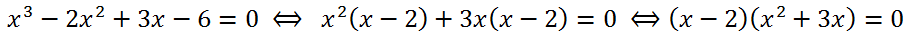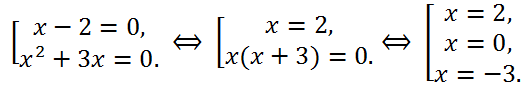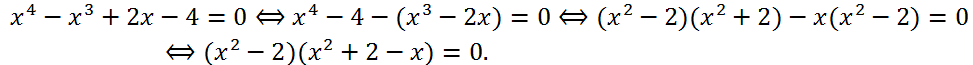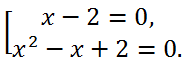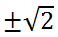Общие приемы решения уравнений

Решение уравнений методом замены переменной

Пример 1. Решить уравнение x⁸ + 15x⁴ - 16 = 0.

Решение.

Введем новую переменную t = x⁴. Тогда исходное уравнение примет вид t² + 15t - 16 = 0.

Корни полученного квадратного уравнения легко находятся по известным формулам t₁ = 1, t₂ = -16.

Теперь для найденных значений t, найдем соответствующие значения x.

Если t = 1   <=>   x⁴ = 1   <=>   x = ±1.

Если t = -16   <=>   x⁴ = -16, но это уравнение корней не имеет. Итак, корни исходного уравнения -1, 1.

Ответ: -1, 1.

Пример 2. Решить уравнение (x² + x - 2)(x² + x - 3) = 12.

Решение.

Положим x² + x - 3 = t. Тогда x² + x - 2 = t+1, и исходное уравнение принимает вид

(t+1)*t = 12   <=>   t² + t - 12 = 0

Решая полученное квадратное уравнение, находим его корни t₁ = -4, t₂ = 3. Таким образом, исходное уравнение эквивалентно совокупности уравнений:



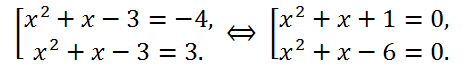
Первое уравнение этой совокупности решений не имеет, а корнями второго, а значит, и исходного являются числа x₁ = -3, x₂ = 2.

Ответ:-3, 2.

Решение уравнений с помощью разложения на множители

Пример 1. Решить уравнение x³ - 2x² + 3x - 6 = 0.

Решение.



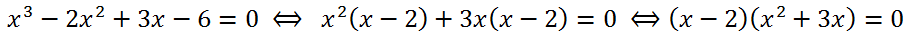
Последнее уравнение эквивалентно совокупности уравнений:

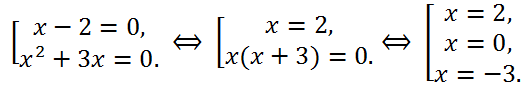
Итак, корнями исходного уравнения являются числа x₁=2, x₂=0, x₃= -3.

Ответ: -3, 0, 2.

Пример 2. Решить уравнение x⁴ - x³ + 2x - 4 = 0.

Решение.



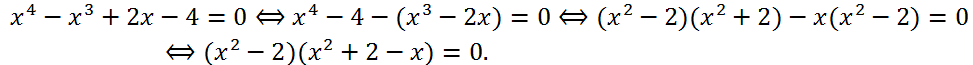
Последнее уравнение эквивалентно совокупности уравнений:



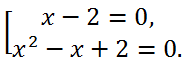
Последнее уравнение совокупности корней не имеет, а корни первого, а значит, и исходного уравнения числа

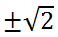Ответ: -√2, √2.