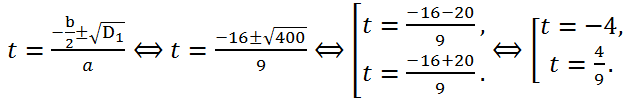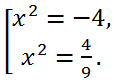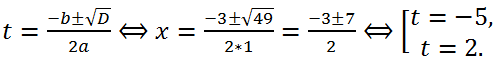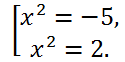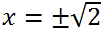Пример 4.
Решить квадратное уравнение x
2 + 12x + 36 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 12, c = 36.
Так как b = 12 - четное число, то вычислим дискриминант D
1 :
D
1 = (b/2)
2 - ac = 6
2 - 1*36 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = (-6)/1 = -6.
Это уравнение можно решить и без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
x
2 + 12x + 36 = 0 <=> (x+6)
2 = 0 <=> x = -6.
Ответ: -6.
Пример 5.
Решить квадратное уравнение 4x
2 -28x + 49 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.
Так как b = -28 - четное число, то вычислим дискриминант D
1 :
D
1 = (b/2)
2 - ac = (-14)
2 - 4*49 = 196-196 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = 14/4 = 7/2.
Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
4x
2 -28x + 49 = 0 <=> (2x-7)
2 = 0 <=> 2x = 7 <=> x = 7/2.
Ответ: 7/2.
Пример 6.
Решить уравнение
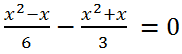 Решение.
Решение.
Приведем к общему знаменателю левую часть уравнения:
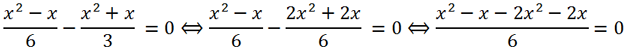
Умножив обе части уравнения на -6, получим x
2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
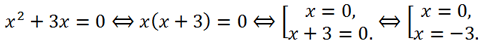 Ответ:
Ответ: -3, 0.
Пример 7.
Решить уравнение
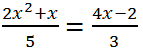 Решение.
Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:
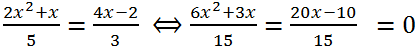
Умножив обе части уравнения на 15, получим:
6x
2 + 3x = 20x-10 <=> 6x
2 + 3x - 20x + 10 = 0 <=> 6x
2 - 17x + 10 = 0.
Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10.
D = b
2 - 4ac = (-17)
2 - 4*6*10 = 289 - 240 = 49 > 0, следовательно, уравнение имеет два действительных корня:
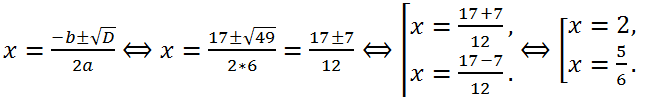 Ответ:
Ответ: 5/6, 2.
Пример 8.
Решить уравнение
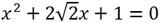 Решение.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.
Так как b = 2√2, то есть b делится на 2 (b/2 = √2), вычислим дискриминант D
1:
D
1 = (
)
2 - ac = (√2)
2 - 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.
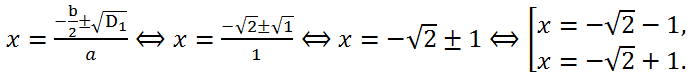 Ответ:
Ответ: -√2-1, -√2+1.
Пример 9.
Решить квадратное уравнение
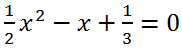 Решение.
Решение.
Умножим левую и правую части уравнения на 6:
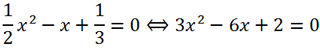
Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.
Так как b = -6, то есть b делится на 2 (b/2 = -3), вычислим дискриминант D
1:
D
1 = (b/2)
2 - ac = 3
2 - 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.
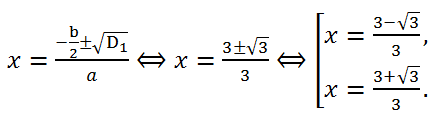 Ответ:
Ответ: 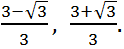 Пример 10.
Пример 10.
Решить уравнение x
4 - 17x
2 + 16 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x
2 => x
4 = t
2, перейдем к эквивалентному исходному квадратному уравнению:
x
4 - 17x
2 + 16 = 0 <=> t
2 - 17t + 16 = 0
Вычислим дискриминант квадратного трехчлена: a = 1, b = -17, c = 16,
D = b
2 - 4ac = (-17)
2 - 4*1*16 = 289-64 = 225 > 0, следовательно, уравнение имеет два действительных корня.
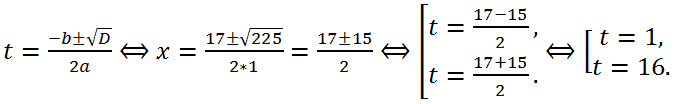
По найденным значениям t, решая уравнения x
2 = t, найдем корни исходного биквадратного уравнения:
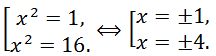
Таким образом, исходное уравнение имеет 4 действительных корня.
Ответ: -4, -1, 1, 4.
Пример 11.
Решить уравнение 9x
4 + 32x
2 - 16 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x
2 => x
4 = t
2, перейдем к эквивалентному исходному квадратному уравнению:
9x
4 + 32x
2 - 16 = 0 <=> 9t
2 + 32t - 16 = 0
Вычислим дискриминант квадратного трехчлена. У нас a = 9, b = 32, c = -16.
Так как b = 32, то есть b делится на 2 (b/2 = 16), вычислим дискриминант D
1:
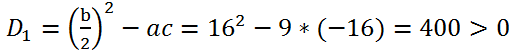
Cледовательно, уравнение имеет два действительных корня.
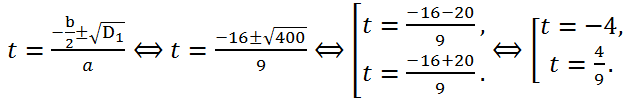
По найденным значениям t, решая уравнения x
2 = t, найдем корни исходного биквадратного уравнения:
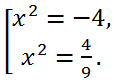
Первое уравнение x
2 = -4 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x =
.
Ответ: -2/3, 2/3.
Пример 12.
Решить уравнение x
4 + 3x
2 - 10 = 0.
Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x
2 => x
4 = t
2, перейдем к эквивалентному исходному квадратному уравнению:
x
4 + 3x
2 - 10 = 0 <=> t
2 + 3t - 10 = 0
Вычислим дискриминант полученного квадратного трехчлена: a = 1, b = 3, c = -10,
D = b
2 - 4ac = 3
2 - 4*1*(-10) = 9+40 = 49 > 0, следовательно, уравнение имеет два действительных корня:
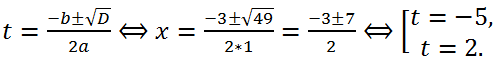
По найденным значениям t, решая уравнения x
2 = t, найдем корни исходного биквадратного уравнения:
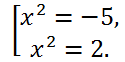
Первое уравнение x
2 = -5 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня
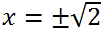 Ответ:
Ответ: -√2, √2.
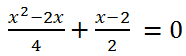 Решение.
Решение.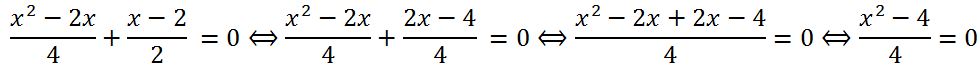
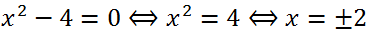
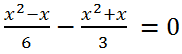
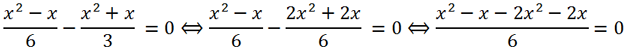 Умножив обе части уравнения на -6, получим x2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
Умножив обе части уравнения на -6, получим x2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители: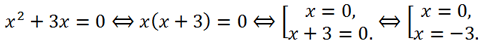 Ответ: -3, 0.
Ответ: -3, 0.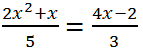 Решение.
Решение.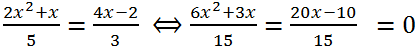
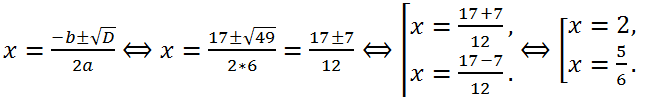
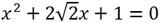
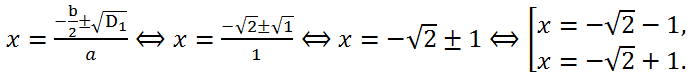
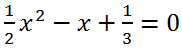
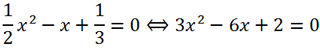
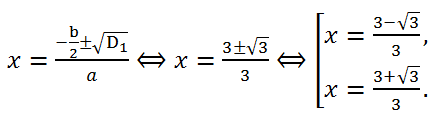
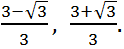
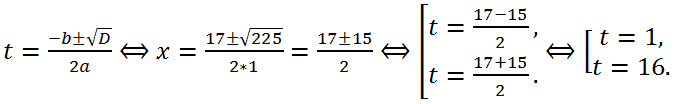
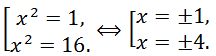
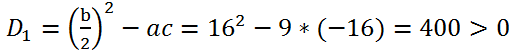 Cледовательно, уравнение имеет два действительных корня.
Cледовательно, уравнение имеет два действительных корня.