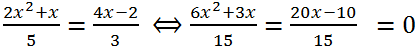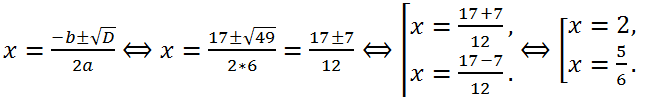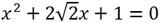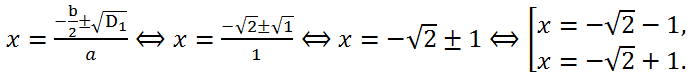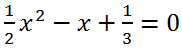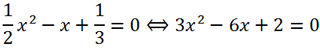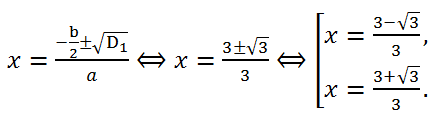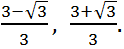Покажем, как вывести эти формулы:
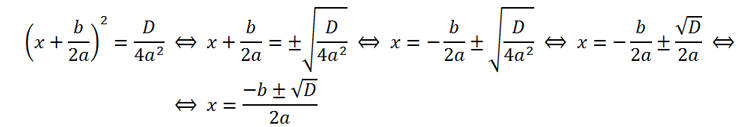
Последнюю формулу можно существенно упростить в случае, если
b делится на 2, то есть b = 2k. Тогда формула для корней квадратного уравнения будет иметь вид
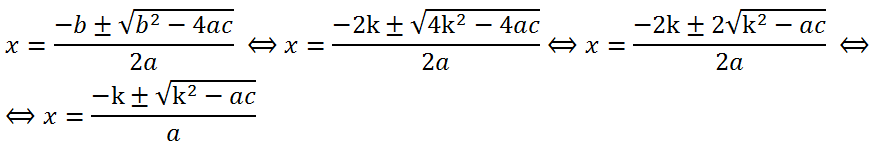
Здесь k = b/2.
Полученную формулу для корней квадратного уравнения в случае четного коэффициента b можно переписать и без использования буквы k:
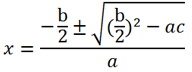
или
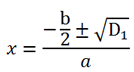
где D
1 = (
)
2 - ac.
Очевидно, полученные формулы для корней полных квадратных уравнений можно использовать и для решения неполных уравнений, хотя проще использовать способы решения неполных квадратных уравнений.
Примеры решения квадратных уравнений
Пример 1.
Решить квадратное уравнение 4x
2 -28x + 49 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.
Так как b = -28 - четное число, то вычислим дискриминант D
1 :
D
1 = (
)
2 - ac = (-14)
2 - 4*49 = 196 - 196 = 0.
Cледовательно, уравнение имеет единственный корень x = (b/2)/2 = 14/2 = 7.
Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
4x
2 -28x + 49 = 0 <=> (2x - 7)
2 = 0 <=> 2x = 7 <=> x = 7/2.
Ответ: 7/2.
Пример 2.
Решить уравнение
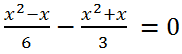 Решение.
Решение.
Приведем к общему знаменателю левую часть уравнения:
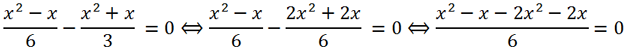
Умножив обе части уравнения на -6, получим x
2 + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
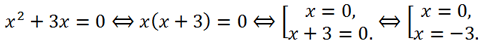 Ответ:
Ответ: -3, 0.
Пример 3.
Решить уравнение
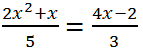 Решение.
Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:
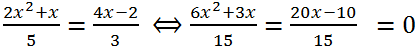
Умножив обе части уравнения на 15, получим:
6x
2 + 3x = 20x-10 <=> 6x
2 + 3x - 20x + 10 = 0 <=> 6x
2 - 17x + 10 = 0.
Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10.
D = b
2 - 4ac = (-17)
2 - 4*6*10 = 289 - 240 = 49 > 0, следовательно, уравнение имеет два действительных корня:
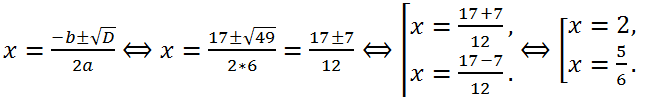 Ответ:
Ответ: 5/6, 2.
Пример 4.
Решить уравнение
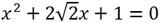 Решение.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.
Так как b = 2√2, то есть b делится на 2 (b/2 = √2), вычислим дискриминант D
1:
D
1 = (
)
2 - ac = (√2)
2 - 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.
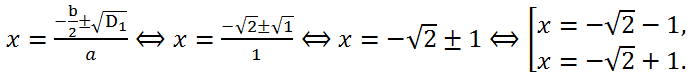 Ответ:
Ответ: -√2-1, -√2+1.
Пример 5.
Решить квадратное уравнение
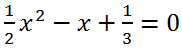 Решение.
Решение.
Умножим левую и правую части уравнения на 6:
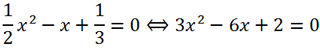
Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.
Так как b = -6, то есть b делится на 2 (b/2 = -3), вычислим дискриминант D
1:
D
1 = (b/2)
2 - ac = 3
2 - 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.
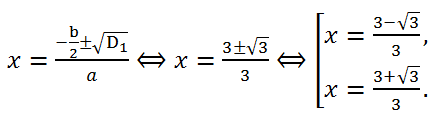 Ответ:
Ответ: 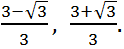
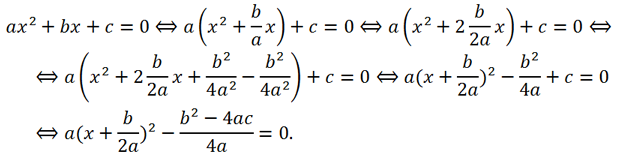
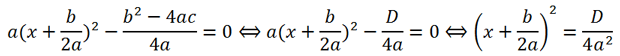
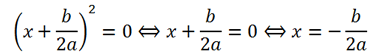
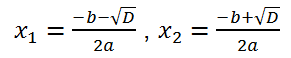
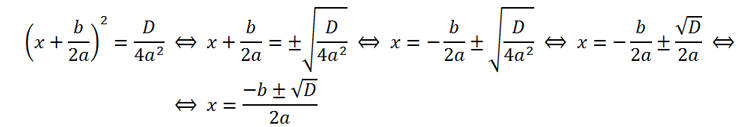
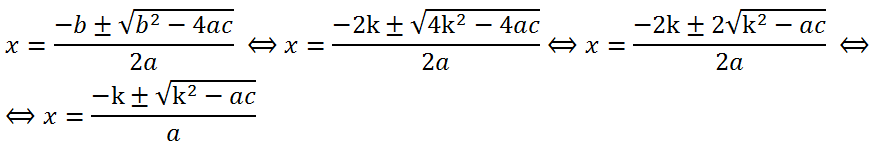 Здесь k = b/2.
Полученную формулу для корней квадратного уравнения в случае четного коэффициента b можно переписать и без использования буквы k:
Здесь k = b/2.
Полученную формулу для корней квадратного уравнения в случае четного коэффициента b можно переписать и без использования буквы k: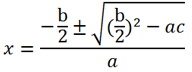 или
или
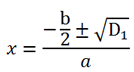 где D1 = (
где D1 = (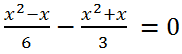 Решение.
Решение.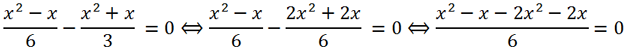
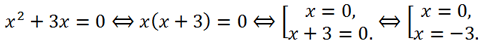 Ответ: -3, 0.
Ответ: -3, 0.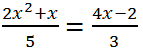 Решение.
Решение.