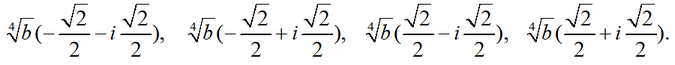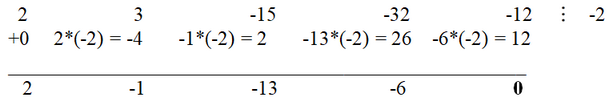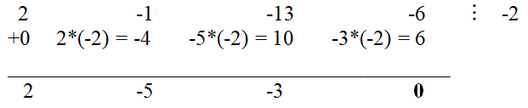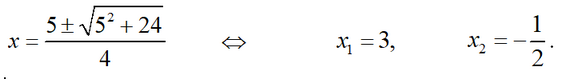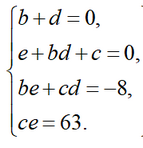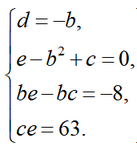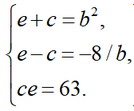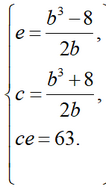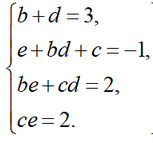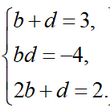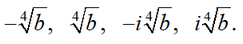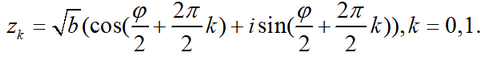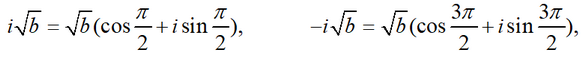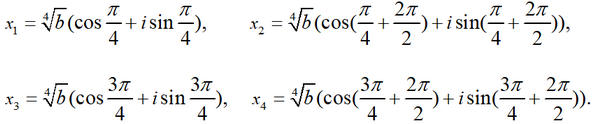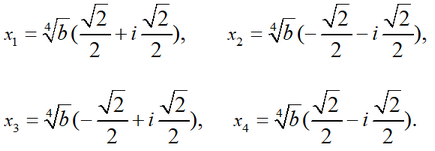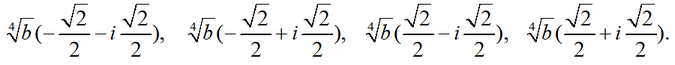Решение уравнений четвертой степени методом разложения на множители

Согласно основной теореме алгебры, уравнение четвертой степени всегда имеет 4 корня (с учётом кратности). Если корнем является комплексное число, то и комплексно сопряженное тоже будет его корнем. Таким образом, многочлен четвертой степени с действительными коэффициентами a(x) = a₀*x⁴ +a₁*x³ + a₂*x² + a₃*x + a₄, a₀ ≠ 0, всегда можно представить в виде произведения своего старшего коэффициента a₀ и нескольких многочленов с действительными коэффициентами: линейных вида x-x₀, соответствующих его действительным корням, и квадратичных, вида x² + bx + c, соответствующих произведениям сопряженных комплексных корней.
Таким образом, приравнивая каждый множитель в разложении к нулю, найдем все корни уравнения. Рассмотрим решение уравнений четвертой степени методом разложения на множители на примерах.

Примеры решения уравнений четвертой степени методом разложения на множители

Пример 1.
Решить уравнение 2x⁴ + 3x³ - 15x² - 32x - 12 = 0.
Решение.
Делителями свободного члена являются числа: ±1, ±2, ±3, ±4, ±6, ±12. Целочисленные корни уравнения нужно искать среди них. Простой подстановкой убеждаемся, что корнем уравнения является число -2. Следовательно, исходное уравнение равносильно (x + 2)*(2x³ + bx² + cx + d) = 0.
Чтобы найти многочлен 2x³ + bx² + cx + d, нужно левую часть исходного уравнения разделить на x+2. Для деления многочлена на двучлен будем использовать схему Горнера.


Таким образом, 2x⁴ + 3x³ - 15x² - 32x - 12 =  (x + 2)(2x³ - x² - 13x - 6). Следовательно, исходное уравнение эквивалентно

(x + 2)(2x³ - x² - 13x - 6)= 0.

Аналогично решаем кубическое уравнение 2x³ - x² - 13x - 6 = 0.
С помощью подстановки убеждаемся, что -2 также является корнем кубического уравнения, Следовательно, -2 - это корень кратности 2. Снова используем схему Горнера для деления на x+2:


Осталось решить получившееся квадратное уравнение 2x² - 5x² - 3 = 0. Его корни:
Ответ: -2, -1/2 , 3.

Пример 2.
Решить уравнение x⁴ - 8x + 63 = 0.
Решение.
Попробуем разложить левую часть уравнения на 2 квадратичных множителя: x⁴ - 8x + 63 = (x² + bx + c)(x² + dx + e).
Будем находить неизвестные величины b, c, d, e методом неопределенных коэффициентов. Перемножим две скобки и приравняем коэффициенты при одинаковых степенях x, получим такую систему уравнений:
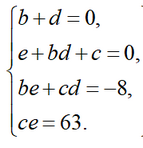
Выразим неизвестную d через b и подставим в уравнения системы:
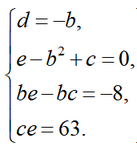
Отсюда
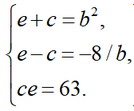
Складывая и вычитая первые два уравнения системы, получим выражения для e и c через b:
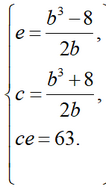
И наконец, подставив выражения для для e и c в третье уравнение, получаем уравнение относительно b

b⁶ - 63*4*b² - 64 = 0.

Простой подстановкой убеждаемся, что b=4 является корнем уравнения. Следовательно, d = -4, e = 7, c = 9. Таким образом, получаем разложение

x⁴ - 8x + 63 =(x² + 4x + 9)(x² - 4x + 7).

Приравнивая каждую скобку к нулю и решая получившиеся квадратные уравнения, находим решения исходного уравнения:

x_1,2 = -2±i√5;     x_3,4 = 2±i√3.

Ответ: -2-i√5, -2+i√5, 2-i√3, 2+i√3.

Еще один пример на применение метода неопределенных коэффициентов.
Пример 3. Решить уравнение x⁴ + 3x³ - x² + 2x + 2 = 0.
Решение.
Разложим левую часть уравнения на 2 квадратичных множителя: x⁴ +3x³ - x² + 2x + 2 = (x² + bx + c)(x² + dx + e).
Перемножив две скобки и приравняв коэффициенты при одинаковых степенях x, получим такую систему уравнений:
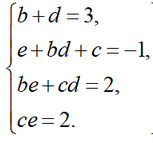
Так как ce=2, то если предположить, что c и e целые числа, то возможны 2 варианта с=±2, так как вариант с=±1 просто меняет порядок квадратичных множителей. Легко убедиться, что решение системы существует только при e=2, тогда c=1. Подставив эти значения в систему, получим
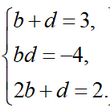
Отсюда b = -1, d = 4. Таким образом, получаем разложение

x⁴ +3x³ - x² + 2x + 2 = (x² - x + 1)(x² + 4x + 2).

Приравнивая каждую скобку к нулю и решая получившиеся квадратные уравнения, находим решения исходного уравнения:

x_1,2 = (1±i√3)/2;     x_3,4 = -2±√2.

Ответ: -2-√2, -2+√2, (1-i√3)/2, (1+i√3)/2.

Пример 4.
Решить уравнение x⁴ - b = 0, где b≥0.
Решение.
Разложим на множители левую часть уравнения по формуле разности квадратов:

(x² -√b)(x² +√b) = 0.

Приравнивая каждую скобку к нулю, получим x² = √b или x² = √-b.
Отсюда
Ответ: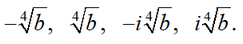

Пример 5.
Решить уравнение x⁴ + b = 0, где b≥0.
Решение.
Разложим на множители левую часть уравнения по формуле разности квадратов:

(x² -√(-b))(x² +√(-b)) = 0  или   (x² -i√b)(x² +i√b) = 0.

Приравнивая каждую скобку к нулю, получим

x² = i√b   или   x² = -i√b.

Как известно, корень 2-ой степени из комплексного числа z,

z = r *(cosφ + isinφ)

имеет 2 комплексных значения √z=z_k , k=0,1, где
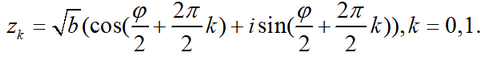
Так как
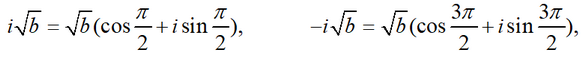
для квадратных корней из i√b и -i√b получаем выражения
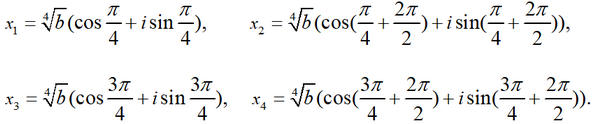
Отсюда, учитывая, что cos(π/4)=√2/2, sin(π/4)=√2/2, cos(3π/4)=-√2/2, sin(3π/4)=√2/2, получаем окончательные выражения для корней исходного уравнения:

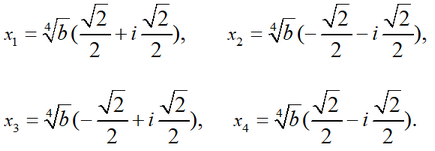Ответ: