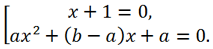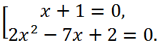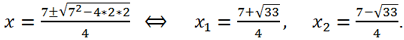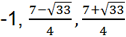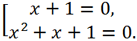Решение симметрических кубических уравнений

Симметрические уравнения 3 степени имеют вид: ax³ + bx² + bx + a = 0, a ≠ 0.
Многочлен в левой части таких уравнений всегда можно разложить на множители следующим образом:
ax³ + bx² + bx + a = a(x³ + 1) + bx(x + 1) =
= a(x + 1)(x² - x + 1) + bx(x + 1) = (x + 1)(ax² + (b - a)x + a).
Следовательно, исходное уравнение равносильно совокупности уравнений:


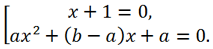
Таким образом, решением исходного уравнения всегда является число -1, а оставшиеся корни являются корнями квадратного уравнения ax² + (b - a)x + a = 0.
Рассмотрим решение симметрических уравнений 3 степени на примерах.

Примеры решения симметрических кубических уравнений

Пример 1.
Решить уравнение 2x³ - 5x² - 5x + 2 = 0.
Решение.
Разложим на множители левую часть исходного уравнения:
2x³ - 5x² - 5x + 2 = 2(x + 1)(x² - x + 1) - 5x(x + 1) = (x + 1)(2x² - 2x + 2 - 5x) = (x + 1)(2x² - 7x + 2).
Итак, исходное уравнение равносильно совокупности


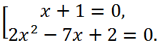
Первое уравнение совокупности имеет корень -1, второe уравнение решаем по формулам корней квадратного уравнения:

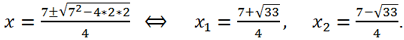Ответ:
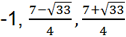Пример 2.
Найти действительные корни уравнения x³ + 2x² + 2x + 1 = 0.
Решение.
x³ + 2x² + 2x + 1 = (x + 1)(x² - x + 1) + 2x(x + 1) = (x + 1)(x² - x + 1 + 2x) = (x + 1)(x² + x + 1). Итак, исходное уравнение равносильно совокупности


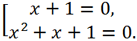
Первое уравнение совокупности имеет корень -1, второe уравнение действительных корней не имеет, так как дискриминант D = 1 - 4 = -3  <  0.
Ответ: -1.