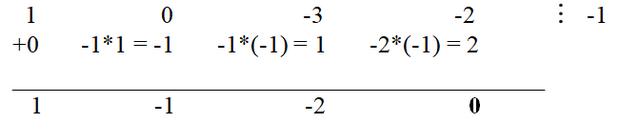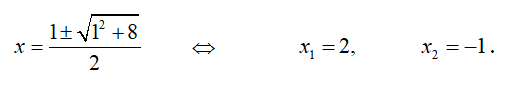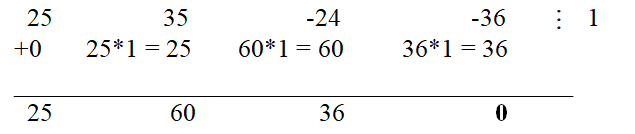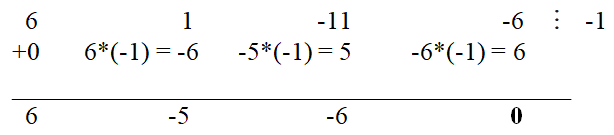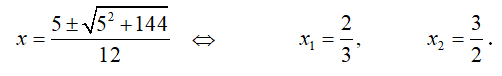Разложение на множители многочлена третьей степени

Многочлен 3 степени a(x) = a₀*x³ + a₁*x² + a₂*x + a₃, a₀ ≠ 0, всегда имеет 3 корня (с учётом кратности). Если комплексное число является корнем многочлена, то и комплексно сопряженное тоже будет его корнем, следовательно, у кубического многочлена всегда существует по крайней мере один действительный корень. Рассмотрим разложение на множители многочленов третьей степени на примерах.

Примеры разложения на множители многочлена третьей степени

Пример 1.
Разложить на множители многочлен x³ - 3x - 2.
Решение.
Делители свободного члена: ±1, ±2. Значит, корни многочлена нужно искать среди них. Простой подстановкой убеждаемся, что корнем многочлена является число -1. Значит, исходный многочлен надо разделить на x + 1.
Воспользуемся схемой Горнера:


Таким образом, x³ - 3x - 2= (x + 1)(x² - x - 2). Чтобы найти оставшиеся 2 корня многочлена, решаем квадратное уравнение x² - x - 2 = 0:

Следовательно, x³ - 3x - 2 = (x + 1)(x² - x - 2) = (x + 1)²(x - 2).
Ответ: x³ - 3x - 2= (x + 1)²(x - 2).

Пример 2.
Разложить на множители многочлен 25x³ + 35x² - 24x - 36.
Решение.
Делители свободного члена: ±1, ±2, ±3, ... .
Делители старшего коэффициента: ±1, ±5, ±25.
Значит, корни исходного многочлена будем искать среди чисел: ±1, ±2, ±3, ... , ±1/2,  ±1/5; ... . Снова простой подстановкой убеждаемся, что 1 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x - 1:


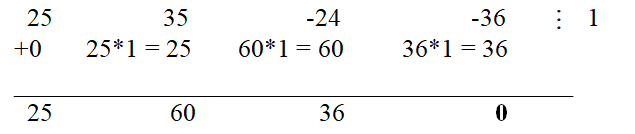
Таким образом, 25x³ + 35x² - 24x - 36= (x + 1)(25x² + 60x + 36). Но квадратный трехчлен 25x² + 60x + 36 = (5x + 6)².
Ответ: 25x³ + 35x² - 24x - 36= (x - 1)(5x + 6)².

Пример 3.
Разложить на множители многочлен 6x³ + x² - 11x - 6.
Решение.
Простой подстановкой убеждаемся, что -1 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x + 1:


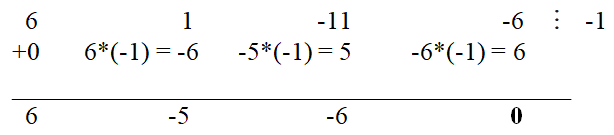
Решая квадратное уравнение 6x² - 5x - 6 = 0, получаем,


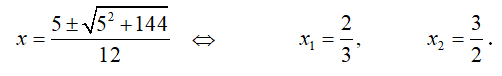
Следовательно, 6x² - 5x - 6 = 6(x - 2/3)(x - 3/2). Таким образом, 6x³ + x² - 11x - 6 = 6(x + 1)(x - 2/3)(x - 3/2).
Ответ: 6x³ + x² - 11x - 6 = (x + 1)(3x - 2)(2x - 3).