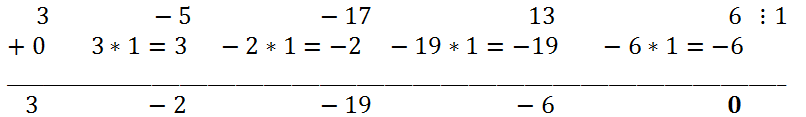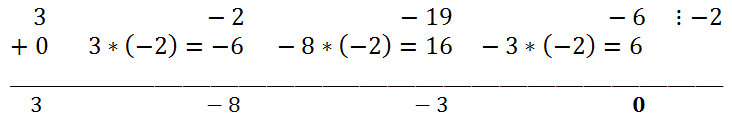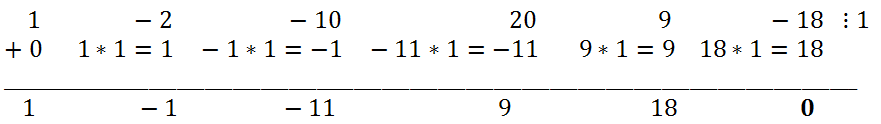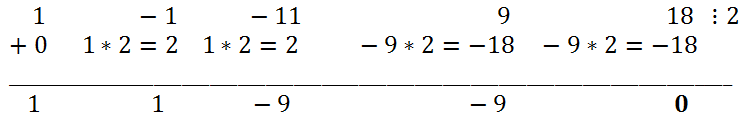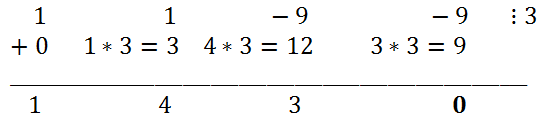Примеры разложения многочленов на множители
Пример 1.
Разложить на множители многочлен 3x
4 - 5x
3 - 17x
2 + 13x + 6.
Решение.
Многочлен четвертой степени может иметь самое большее 4 разных корня. Попытаемся найти эти корни.
Делители свободного члена: ±1, ±;2, ±3, ±6.
Делители старшего коэффициента: ±1, ±3.
Следовательно, рациональные корни многочлена можно искать среди чисел ±1, ±;2, ±3, ±6,
.
Подставив в многочлен x = 1, убеждаемся, что x = 1 является корнем многочлена. Значит, исходный многочлен надо разделить на x-1. Для этого воспользуемся
схемой Горнера.
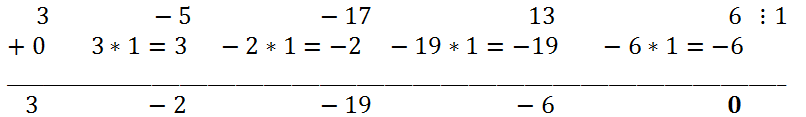
Итак, 3x
4 - 5x
3 - 17x
2 + 13x + 6=(x - 1)(3x
3 - 2x
2 - 19x - 6).
Теперь надо разложить на множители многочлен 3x
3 - 2x
2 - 19x - 6.
Делители свободного члена: ±1, ±;2, ±3, ±6.
Делители старшего коэффициента: ±1, ±3.
То есть, его рациональные корни можно искать среди тех же чисел, что и корни исходного многочлена:
±1, ±;2, ±3, ±6,
.
Подставив в многочлен x = -2, убеждаемся, что x = -2 является корнем многочлена. Значит, исходный многочлен надо разделить на x + 2.
Воспользуемся схемой Горнера.
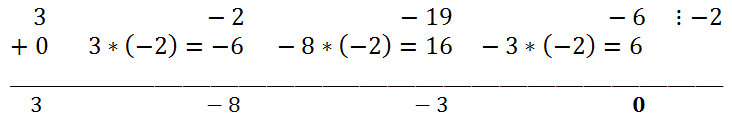
Следовательно, 3x
3 - 2x
2 - 19x - 6 = (x + 2)(3x
2 - 8x - 3). Попробуем также понизить степень многочлена 3x
2 - 8x - 3, хотя можно просто решить квадратное уравнение.
Делители свободного члена: ±1, ±;2, ±3.
Делители старшего коэффициента: ±1, ±3.
То есть, его рациональные корни можно искать среди чисел ±1, ±;2, ±3,
. Подстановкой проверяем, что подходят числа
и 3. Все корни найдены, значит найдено и разложение на множители:
3x
4 - 5x
3 - 17x
2 + 13x + 6 = 3(x - 1)(x + 2)(x - 3)(x + 1/3).
Ответ: 3x
4 - 5x
3 - 17x
2 + 13x + 6 = (x - 1)(x + 2)(x - 3)(3x + 1).
Пример 2.
Разложить на множители многочлен x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18.
Решение.
Многочлен пятой степени может иметь самое большее 5 разных корней. Попытаемся найти эти корни. Так как делитель старшего коэффициента равен 1, рациональные корни многочлена можно искать среди делителей свободного члена: ±1, ±;2, ±3, ±6, ±9, ±18. Подставив в многочлен x = 1, убеждаемся, что x = 1 является корнем многочлена. Значит, исходный многочлен надо разделить на x-1. Снова воспользуемся схемой Горнера.
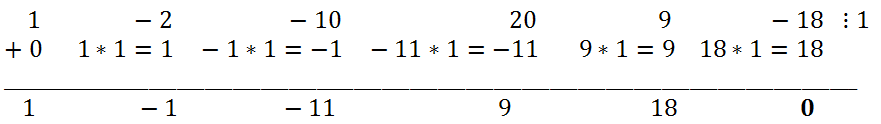
Итак, x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18 = (x - 1)(x
4 - x
3 - 11x
2 + 9x + 18). Аналогичным образом, рациональные корни многочлена x
4 - x
3 - 11x
2 + 9x + 18 можно искать среди тех же делителей свободного члена:±1, ±;2, ±3, ±6, ±9, ±18. Подставив в многочлен x=2, убеждаемся, что x=2 является корнем многочлена. Значит, этот многочлен надо разделить на x-2.
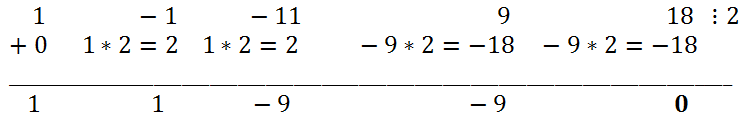
Таким образом, x
4 - x
3 - 11x
2 + 9x + 18 = (x - 2)(x
3 + x
2 - 9x - 9). Корни многочлена x
3 + x
2 - 9x - 9 можно искать среди делителей свободного члена 9:±1, ±3, ±9. Легко видеть, что x = 3 является корнем многочлена. Понизим степень этого многочлена, разделив его на x-3.
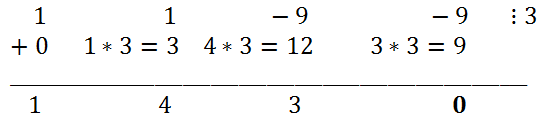
Следовательно, x
3 + x
2 - 9x - 9 = (x - 3)(x
2 + 4x + 3). Корнями квадратного трехчлена x
2 + 4x + 3 являются числа -1 и -3. Процесс поиска корней исходного многочлена завершен.
Ответ: x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18 = (x - 1)(x + 1)(x - 2)(x - 3)(x + 3).
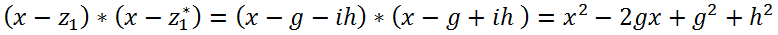 представляет собой квадратичное выражение.
представляет собой квадратичное выражение.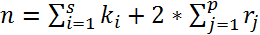 То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.
То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.