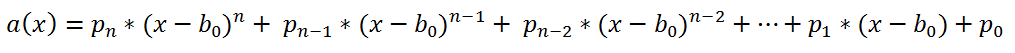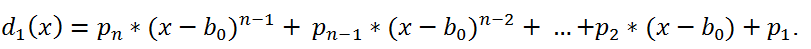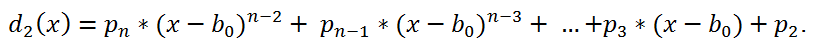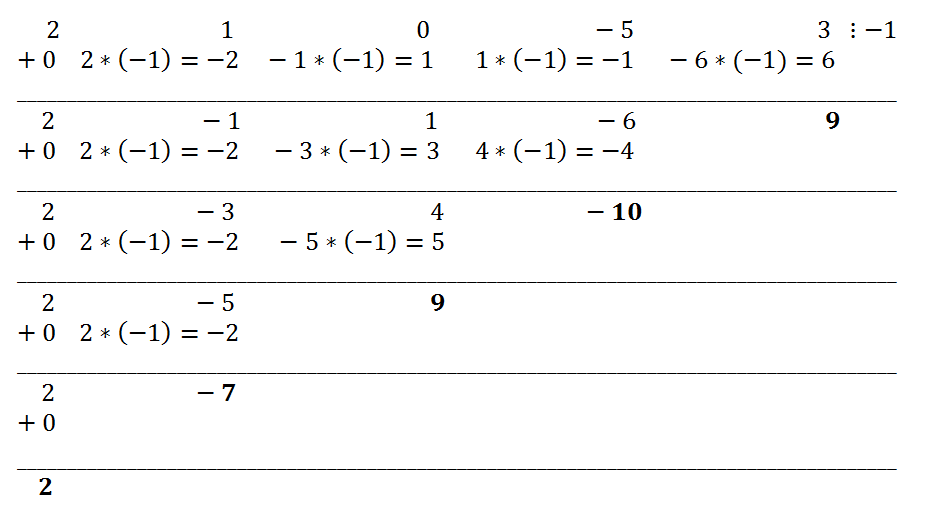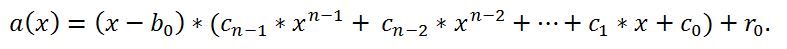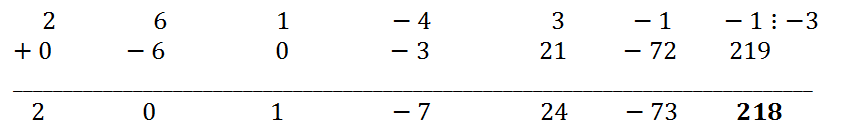Пример 1. Разделить многочлен x
4 - 3x
3 - 3x
2 + 7x + 6 на двучлен x-3 используя схему Горнера.
Решение.
Делимое a(x)=x
4 - 3x
3 - 3x
2 + 7x + 6, b
0=3. В соответствии со схемой Горнера заполняем таблицу
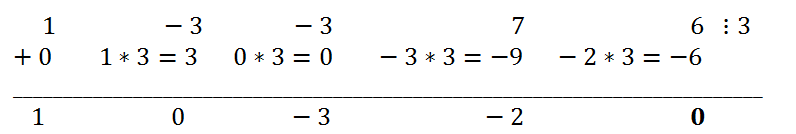
Таким образом, остаток r (это последнее число в третьей строке) равен нулю. Значит, многочлен x
4 - 3x
3 - 3x
2 + 7x + 6 разделился на x - 3 нацело. Частное с(x)=1*x
3 + 0*x
2 - 3x - 2.
Ответ: x
4 - 3x
3 - 3x
2 + 7x + 6=(x
3 - 3x - 2)*(x - 3).
Пример 2. Разделить многочлен 2x
5 + 5x
4 - 4x
3 + 612 на двучлен x + 4 используя схему Горнера.
Решение.
Делимое a(x)= 2x
5 + 5x
4 - 4x
3 + 612, b
0=-4. В соответствии со схемой Горнера заполняем таблицу
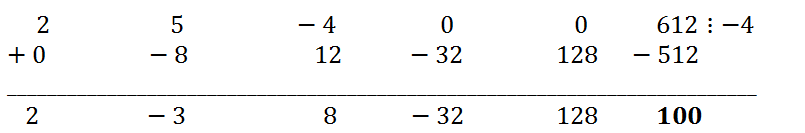
Остаток r = 100 - это последнее число в третьей строке. Частное с(x)=2*x
4 - 3*x
3 - 8*x
2 - 32*x + 128.
Ответ: 2x
5 + 5x
4 - 4x
3 + 612 = (2x
4 - 3x
3 - 8x
2 - 32x + 128)*(x + 4) + 100.
Деление многочлена a(x) на двучлен вида b
1 x - b
0 легко сводится к случаю деления на x - b
0.
Пусть a(x) = (b
1x - b
0)* c(x) + r
0, можно преобразовать это выражение
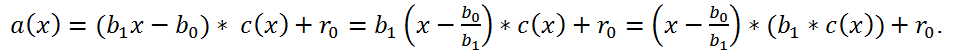
Анализ последнего выражения показывает, что остаток от деления a(x) на b
1x - b
0 тот же самый, что и остаток от деления a(x) на x - b
0/b
1, а коэффициенты частного c(x) получаются из коэффициентов частного от деления на x - b
0/b
1 делением их на b
1.
Пример 3. Разделить многочлен x
3 - 6x
2 + 5x + 2 на двучлен 2x + 1 используя схему Горнера.
Решение.
Так как 2x + 1=2(x + 1/2), с помощью схемы Горнера будем делить исходный многочлен на x + 1/2, затем полученные коэффициенты частного разделим на 2.
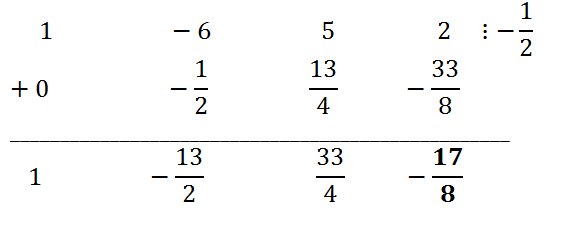
Остаток r
0 = -17/8. Коэффициенты частного получим, разделив коэффициенты в третьей строке таблицы на 2. Таким образом, частное от деления исходного многочлена на 2x + 1
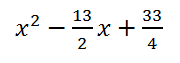
Ответ:
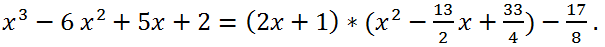 Пример 4.
Пример 4. Разделить многочлен x
5 - x
3 + 2x - 1 на двучлен 3 - 2x.
Решение.
Так как 3 - 2x = - 2(x - 3/2), с помощью схемы Горнера будем делить исходный многочлен на x - 3/2, затем полученные коэффициенты частного разделим на -2.
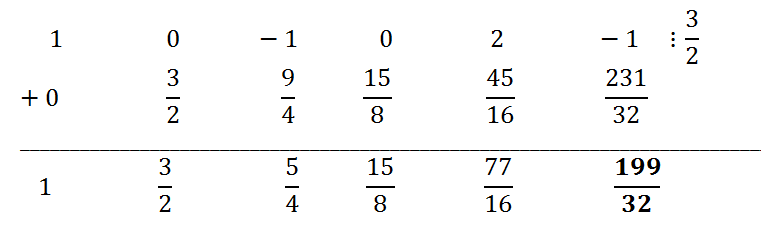
Остаток r
0 = 199/32. Коэффициенты частного получим, разделив коэффициенты в третьей строке таблицы на -2. Таким образом, частное от деления исходного многочлена на 3 - 2x
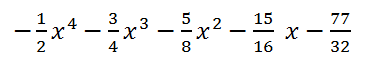
Ответ:
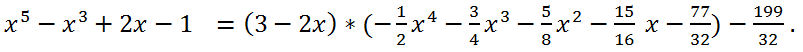
Использование схемы Горнера для разложения многочлена по степеням двучлена
Рассмотрим еще одно применение схемы Горнера – разложение многочлена по степеням двучлена. Для любого многочлена
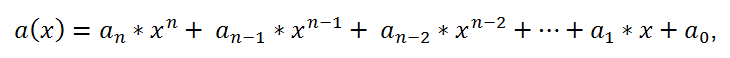
где
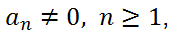
и для любого числа b
0 можно написать разложение a(x) по степеням x - b
0:
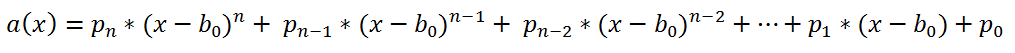
Как видно из этой формулы, чтобы вычислить p
0, необходимо разделить многочлен a(x) на x - b
0 и найти остаток r = p
0 . В частном мы получим многочлен
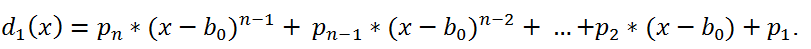
Теперь, чтобы вычислить p
1, необходимо разделить многочлен d
1 (x) на x - b
0 и найти остаток r=p
1. В частном получим многочлен
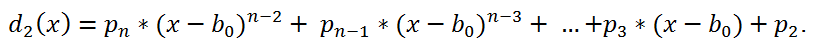
Далее продолжаем деление до тех пор, пока в частном не получится число. Полученный на последнем шаге остаток будет равен p
n-1, а частное d
n=p
n.
На каждом шаге деление на x - b
0 будем проводить с помощью схемы Горнера. При этом очень удобно результаты вычислений записывать в одну общую таблицу. Рассмотрим соответствующие примеры.
Пример 5. Разложить многочлен 2x
4 + x
3 - 5x + 3 по степеням двучлена x + 1.
Решение.
Все вычисления проведем, последовательно заполняя таблицу в соответствии с алгоритмом.
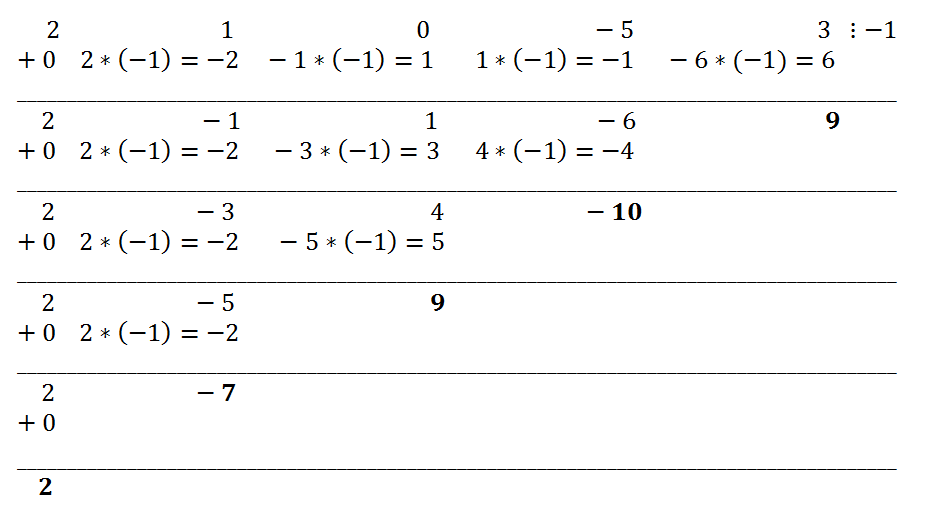
Таким образом, получаем, что остаток от деления исходного многочлена на x+1 равен 9, коэффициенты частного 2,-7,9,-10.
Ответ:
2x
4 + x
3 - 5x + 3 = 2(x + 1)
4 - 7(x + 1)
3 + 9(x + 1)
2 - 10(x + 1) + 9.
Вычисление значения многочлена в заданной точке с помощью схемы Горнера
Еще одна задача, которую можно решать с помощью схемы Горнера – вычисление значения многочлена в заданной точке. Пусть многочлен a(x) делится на двучлен x - b
0 с остатком r
0. То есть
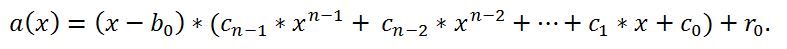
Если в это равенство подставить значение x=b
0, получим a(b
0)=r
0. Таким образом, мы доказали теорему Безу.
Теорема Безу. Если x
0 - произвольное число, то при делении многочлена a(x) на двучлен x-x
0 получается остаток, равный значению многочлена при x=x
0, то есть r
0= a(x
0).
Таким образом, с помощью схемы Горнера можно находить значение многочлена при заданном значении x=x
0 как остаток от деления этого многочлена на двучлен x-x
0. Иногда это сделать гораздо проще, чем подставлять x
0 в исходный многочлен.
У теоремы Безу есть очень важное следствие.
Следствие. Число x
0 является корнем многочлена a(x) тогда и только тогда, когда многочлен a(x) делится нацело на двучлен x-x
0.
Это следствие позволяет проверять, является ли число x
0 корнем многочлена, вычисляя остаток от деления многочлена на двучлен x-x
0.
Пример 6. Вычислить значение многочлена 2x
6 + 6x
5 + x
4 - 4x
3 + 3x
2 - x - 1 при x=-3.
Решение.
Вычислить значение многочлена при x=-3 равносильно найти остаток при делении этого многочлена на x+3. Для этого воспользуемся схемой Горнера
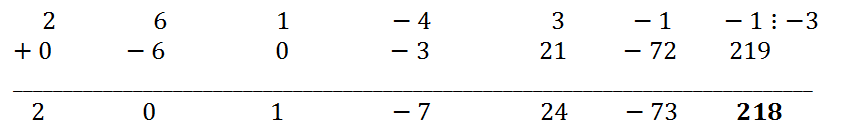
Остаток r (это последнее число в третьей строке) равен 218.
(Частное с(x)=2x
5 + x
3 - 7x
2 + 24x - 73;
2x
6 + 6x
5 + x
4 - 4x
3 + 3x
2 - x - 1=(2x
5 + x
3 - 7x
2 + 24x - 73)*(x+3)+218).
Ответ: 218.
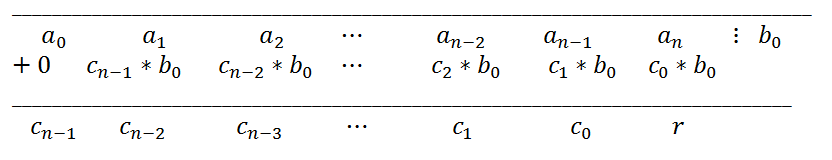
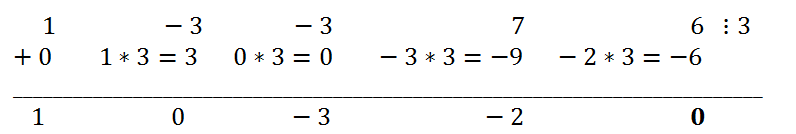
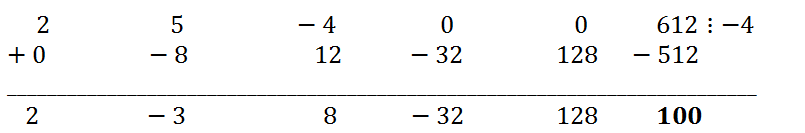
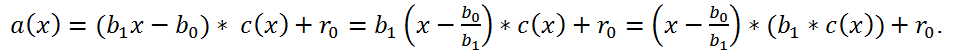
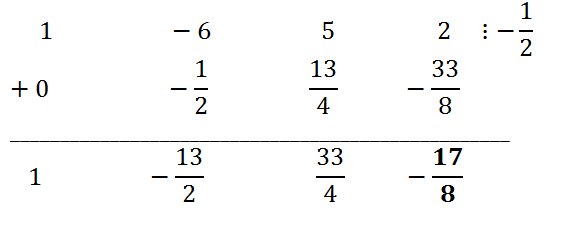
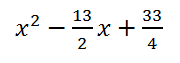
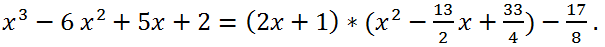
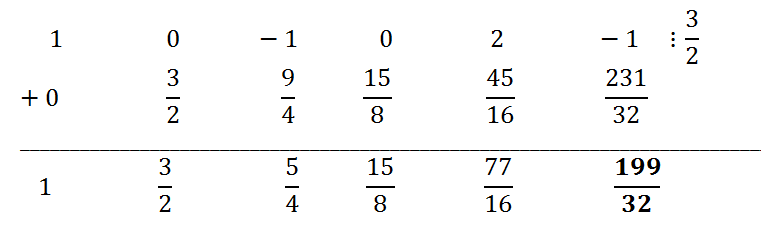
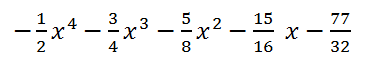
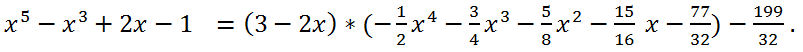
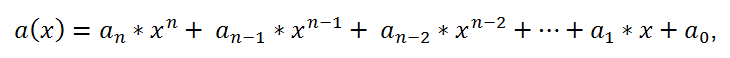
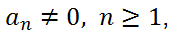 и для любого числа b0 можно написать разложение a(x) по степеням x - b0:
и для любого числа b0 можно написать разложение a(x) по степеням x - b0: