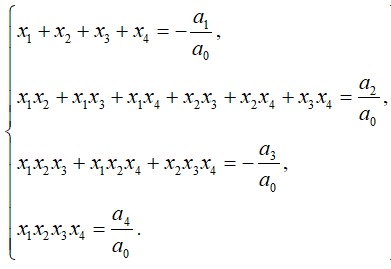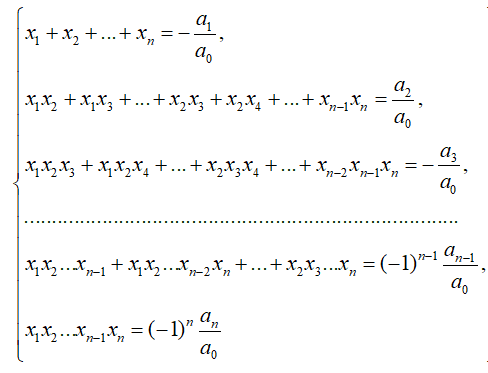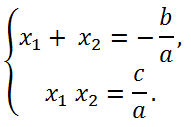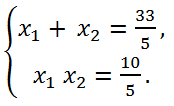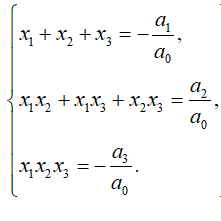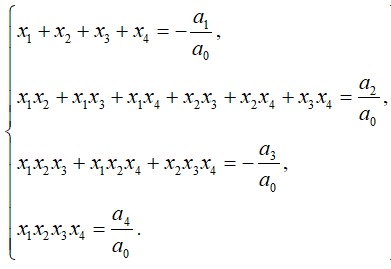Обобщенная теорема Виета

Если числа x₁, x₂,…,x_n – корни многочлена n-ой степени (n равно количеству корней с учетом их кратности)

a₀*xⁿ + a₁*x^n-1 + a₂*x^n-2 + ... + a_n-1*x + a_n, a₀ ≠0,

то справедливы равенства:


Эти равенства называются формулами Виета.
Выпишем их отдельно для корней многочленов второго, третьего и четвертого порядков.

Формулы Виета для корней квадратного трехчлена

Для корней квадратного трехчлена ax² + bx + c справедливы равенства


Формулы Виета для корней квадратного трехчлена позволяют подбирать его целочисленные корни (если они существуют), не решая квадратного уравнения.

Пример 1.
Разложить на множители квадратный трехчлен x² - 2012x + 2011.
Решение.
Легко видеть, что x = 1 является корнем трехчлена. Убеждаемся в этом простой подстановкой. По формуле Виета

x₁x₂ =  = 2011 <=> 1*x₂ = 2011 <=> x₂ = 2011. Следовательно, x² - 2012x + 2011 = (x - 1)(x - 2011).

Ответ: x² - 2012x + 2011 = (x - 1)(x - 2011).

Пример 2.
Разложить на множители квадратный трехчлен 2012x² + 2011x - 1.
Решение.
Простой подстановкой легко проверяется, что x = -1 является корнем квадратного трехчлена. По формуле Виета

x₁x₂ =  <=> -1*x₂ =  <=> x₂ = .

Следовательно, 2012x² + 2011x - 1= 2012(x + 1)(x - ) = (x+1)(2012x-1).
Ответ: 2012x² + 2011x - 1= 2012(x + 1)(x - ) = (x+1)(2012x-1).

Таким образом, очень часто формулы Виета позволяют быстро подобрать целые корни квадратного трехчлена, не проводя громоздких вычислений. Кроме того, по коэффициентам трехчлена можно сделать выводы о знаках корней уравнения. Например, если корни трехчлена существуют, и > 0, то или оба корня положительны, или оба отрицательны.

Пример 3.
Определить знаки корней квадратного уравнения 5x² - 33x + 10 = 0, не решая его.
Решение.
Дискриминант уравнения D = b² - 4ac = 33² - 4*5*10 > 0, следовательно, уравнение имеет два действительных корня. По формулам Виета


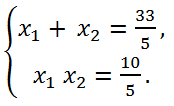
То есть x₁x₂ > 0, значит оба корня имеют одинаковый знак. Но сумма корней > 0, следовательно, оба корня положительные числа.
Ответ: уравнение имеет два положительных корня.

Кроме того, формулы Виета позволяют быстро проверить, является ли заданный набор чисел корнями многочлена. В общем, формулы Виета – это очень полезный инструмент в решении самых разных задач с многочленами. Эти формулы для квадратного трехчлена даже изложены в стихах неизвестным автором:

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи постоянства такого:
Умножишь ты корни - и дробь уж готова:
В числителе c, в знаменателе a,
А сумма корней тоже дроби равна
Хоть с минусом дробь эта, что за беда
В числителе b, в знаменателе a.

Выпишем формулы Виета для многочленов третьего и четвертого порядков.

Формулы Виета для корней многочлена третьего порядка

Если x₁, x₂, x₃ - корни многочлена a₀*x³ + a₁*x² + a₂*x + a₃, то для них справедливы следующие равенства:

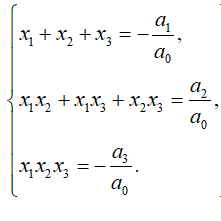
Формулы Виета для корней многочлена четвертого порядка

Если x₁, x₂, x₃, x₄ - корни многочлена a₀*x⁴ + a₁*x³ + a₂*x² + a₃*x + a₄, то для них справедливы равенства: