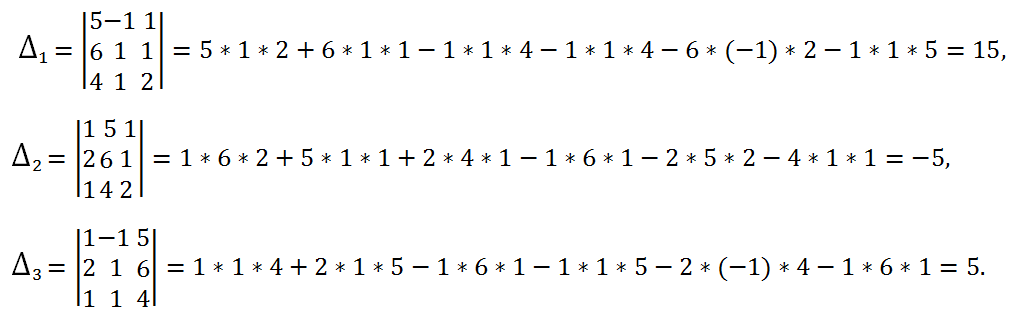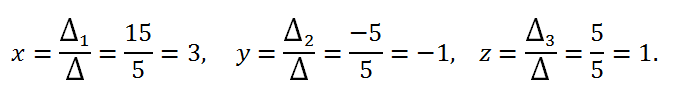Так как вычисление определителей 4-ого и более высоких порядков довольно громоздкая процедура, то нахождение корней системы линейных уравнений по формулам Крамера целесообразно для систем двух или трех уравнений. Выпишем формулы для вычисления определителей второго и третьего порядков.
Определитель второго порядка
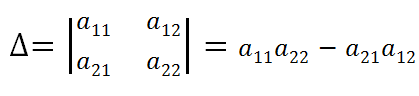
Определитель третьего порядка
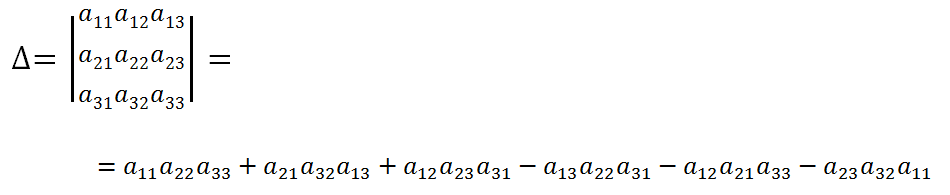
Рассмотрим применение формул Крамера на примерах.
Пример 1. Решить систему
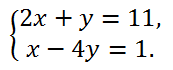 Решение.
Решение.
1. Вычислим определитель этой системы:
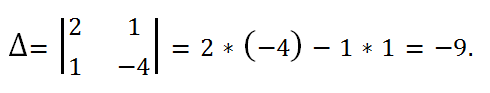
Определитель системы равен -9 < 0, следовательно, система совместна и имеет единственное решение.
2. Вычислим определители
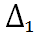
и
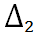
, которые получаются из определителя

заменой первого и второго столбца, соответственно, на столбец свободных членов:
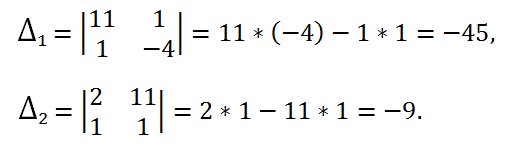
3. По формулам Крамера вычисляем значения неизвестных:
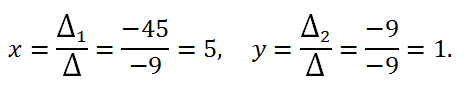
Ответ: x = 5, y = 1.
Пример 2. Решить систему
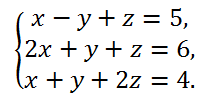 Решение.
Решение.
1. Вычислим определитель этой системы:
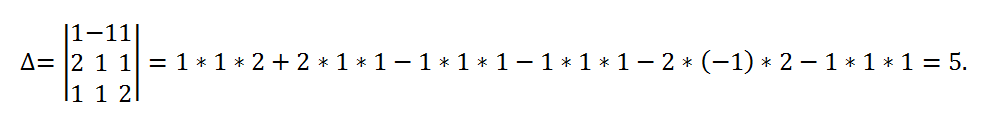
Определитель системы равен 5 < 0, следовательно, система совместна и имеет единственное решение.
2. Вычислим определители
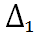
,
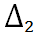
и
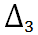
, которые получаются из определителя

заменой первого, второго и третьего столбцов, соответственно, на столбец свободных членов:
3. По формулам Крамера вычисляем значения неизвестных:
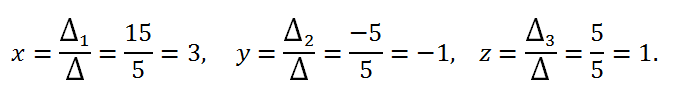
Ответ: x = 3, y = -1, z = 1.
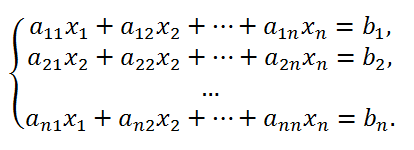
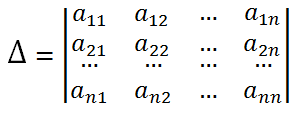
 какой-либо столбец, например, j-ый, столбцом b из свободных членов. Полученный таким образом определитель обозначим
какой-либо столбец, например, j-ый, столбцом b из свободных членов. Полученный таким образом определитель обозначим 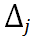 , то есть
, то есть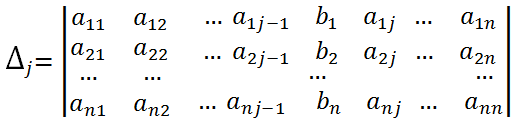
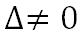 , то эта система совместна и имеет единственное решение, которое находится по формуле Крамера (правило Крамера):
, то эта система совместна и имеет единственное решение, которое находится по формуле Крамера (правило Крамера):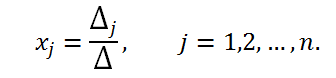
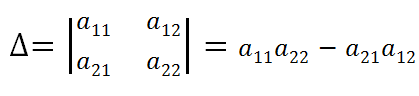
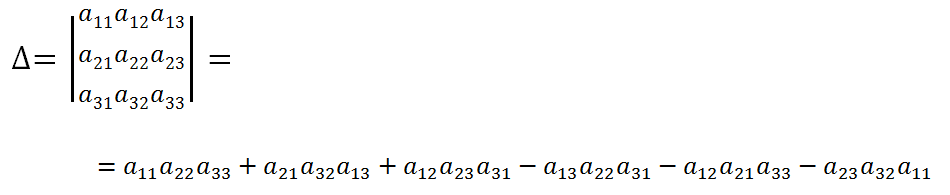
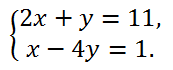
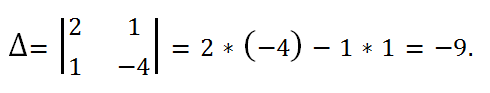
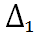 и
и 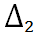 , которые получаются из определителя
, которые получаются из определителя  заменой первого и второго столбца, соответственно, на столбец свободных членов:
заменой первого и второго столбца, соответственно, на столбец свободных членов: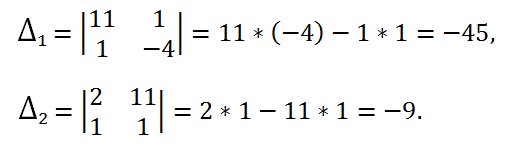
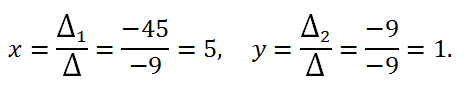
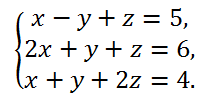
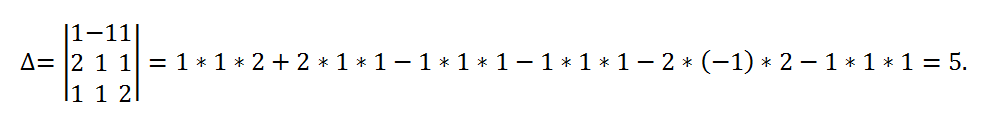
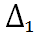 ,
, 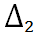 и
и 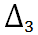 , которые получаются из определителя
, которые получаются из определителя  заменой первого, второго и третьего столбцов, соответственно, на столбец свободных членов:
заменой первого, второго и третьего столбцов, соответственно, на столбец свободных членов: