Центральный угол, вписанный угол
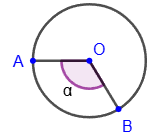
Центральный угол - угол, образованный двумя радиусами: ∠AOB.
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла: ∪AB = ∠AOB.
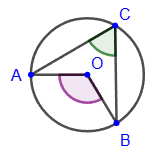
Вписанный угол - угол, образованный двумя хордами, исходящими из одной точки на окружности: ∠ACB.
Вписанный угол равен половине соответствующего центрального угла (другими словами, половине величины дуги, на которую он опирается): ∠AСB = ½∠AOB = ½∪AB.
Свойства углов и дуг:
1) Вписанные углы, опирающиеся на одну и ту же дугу или на равные дуги, равны.
2) Вписанный угол - прямой тогда и только тогда, когда он опирается на диаметр.
3) Равные дуги стягиваются равными хордами.
4) Равные хорды стягивают равные дуги.
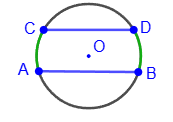
5) Дуги окружности, заключенные между параллельными хордами, равны: ∪AC = ∪BD.