Определения: окружность, хорда, касательная, внутреннее и внешнее касание окружностей, секущая

Окружность

Окружность - геометрическое место точек, равноудаленных от одной точки - центра окружности. Радиус окружности - расстояние от центра окружности до любой точки окружности. Радиусом также называют любой отрезок, соединяющий точку окружности с ее центром.
Хорда окружности - отрезок соединяющий две любые точки на окружности. Диаметр окружности - хорда, проходящая через центр окружности.
На рисунке точка O - центр окружности, отрезок OA (или OB) - радиус окружности, отрезок AB - диаметр окружности, отрезок CD - хорда.

Касательная к окружности

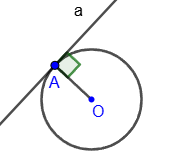
Касательная - это прямая, проходящая через точку на окружности перпендикулярно к радиусу, проведенному в эту точку.
Касательная к окружности не имеет с ней других общих точек, кроме точки касания.
На рисунке прямая a, перпендикулярная к радиусу AO, является касательной. Точка A - точка касания.

Внутреннее касание окружностей

Две окружности касаются друг друга, если они имеют общую касательную в точке, принадлежащей обеим окружностям.
Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной.
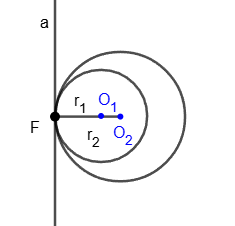
Для расстояния между центрами окружностей справедлива формула: O₁O₂ = r₂ - r₁.

Внешнее касание окружностей

Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной.
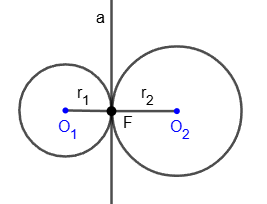
Для расстояния между центрами окружностей справедлива формула: O₁O₂ = r₁ + r₂.

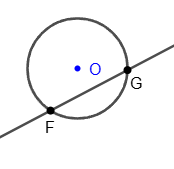
Секущая

Секущая - это прямая, пересекающая окружность в двух точках.