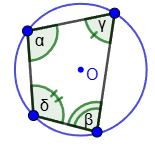
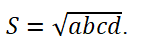Обозначения:
R - радиус описанной окружности;
r - радиус вписанной окружности;
α, β, γ, δ - углы четырехугольника;
a, b, c, d - стороны четырехугольника;
S - площадь четырехугольника.
Четырехугольники, вписанные в окружность. Окружности, описанные вокруг четырехугольника.
Четырехугольник называется вписанным в окружность, если окружность проходит через все четыре вершины четырехугольника. Окружность в этом случае называется описанной вокруг четырехугольника.
1. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов: α+β = γ+δ = 180
∘.
2. Теорема Птолемея.
Для вписанного четырехугольника произведение длин диагоналей равно сумме произведений длин двух пар его противоположных сторон AC*BD = AB*CD + BC*AD.
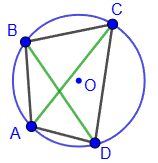
Обратная теорема.
Если произведение длин диагоналей четырехугольника равно сумме произведений длин двух пар его противоположных сторон, то такой четырехугольник можно вписать в окружность.
3. Окружность можно описать
- около параллелограмма тогда и только тогда, когда этот параллелограмм – прямоугольник;
- около ромба тогда и только тогда, когда этот ромб – квадрат;
- около трапеции тогда и только тогда, когда трапеция равнобедренная.
4. Формула Брахмагупты для площади вписанного четырехугольника с полупериметром
p = (a+b+c+d)/2:
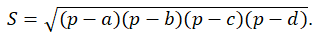
 2. Теорема Птолемея.
2. Теорема Птолемея. Обратная теорема.
Обратная теорема.
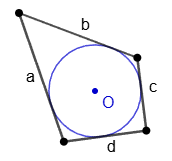
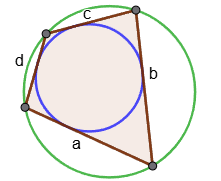
 5. Формула площади описанного четырехугольника через радиус вписанной окружности и стороны четырехугольника:
5. Формула площади описанного четырехугольника через радиус вписанной окружности и стороны четырехугольника: