Треугольники, вписанные в окружность и описанные вокруг окружности

Обозначения:
R - радиус описанной окружности;
r - радиус вписанной окружности;
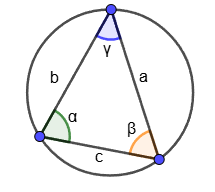
α, β, γ - углы треугольника;
a, b, c - стороны треугольника;
S - площадь треугольника.

Треугольники, вписанные в окружность. Окружности, описанные вокруг треугольника.

Треугольник называется вписанным в окружность, если окружность проходит через все три вершины треугольника. Окружность в этом случае называется описанной вокруг треугольника. Вокруг любого треугольника можно описать окружность.

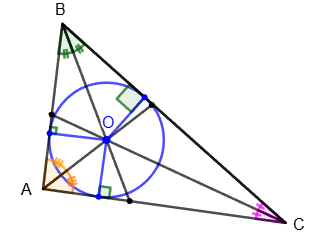
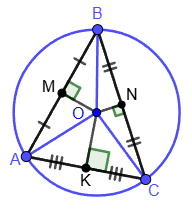
1. Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров:

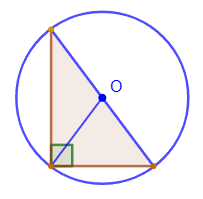
2. Центр описанной вокруг прямоугольного треугольника окружности лежит на середине гипотенузы, а ее радиус равен половине гипотенузы.

3. Формула площади вписанного треугольника через радиус описанной окружности и стороны треугольника:

S = abc/(4R).

4. Теорема синусов:

a/sinα = b/sinβ = c/sinγ = 2R.

Треугольники, описанные вокруг окружности. Окружности, вписанные в треугольники.

Треугольник называется описанным вокруг окружности, если окружность касается всех трех сторон треугольника. Окружность в этом случае называется вписанной в треугольник. В любой треугольник можно вписать окружность.

1. Центр вписанной в треугольник окружности лежит на пересечении биссектрис:

2. Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен:

r = ½(a+b-c).

3. Формула площади описанного треугольника через радиус вписанной окружности и стороны треугольника:

S = ½(a+b+c)*r.