Углы между хордами, касательными и секущими
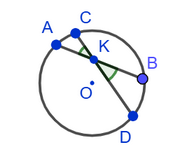
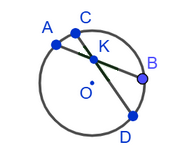
1. Вертикальные углы между пересекающимися хордами равны полусумме величин дуг, заключенных между их сторонами: ∠AKC = ∠BKD = ½(∪AC + ∪BD).
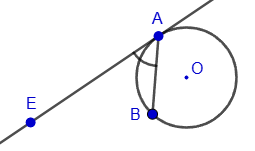
2. Угол между касательной и хордой, исходящих из одной точки окружности, равен половине величины дуги между ними: ∠BAE = ½(∪AB).
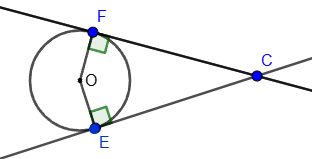
3. Угол между двумя касательными, исходящими из одной точки, равен полуразности величин дуг, заключенных между его сторонами: ∠FCE = ½(∪FDE - ∪FBE).
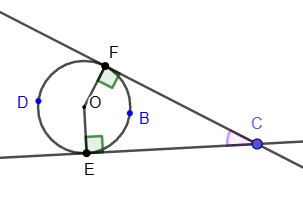
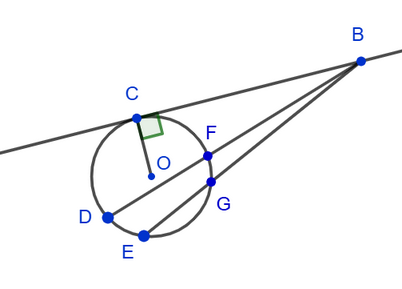
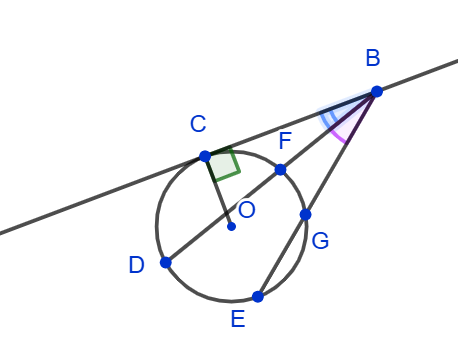
4. Угол между касательной и секущей, исходящих из одной точки, равен полуразности величин дуг, заключенных между его сторонами: ∠DBC = ½(∪CD - ∪CF).
Угол между двумя секущими, исходящими из одной точки, равен полуразности величин дуг, заключенных между его сторонами: ∠DBE = ½(∪DE - ∪FG).
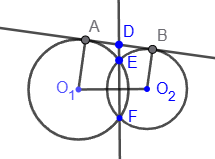
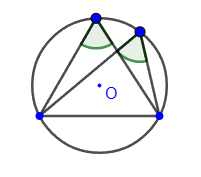
5. Если два равных угла опираются на один и тот же отрезок, то через вершины углов и концы отрезка можно провести окружность:
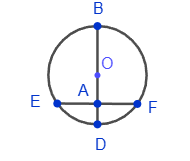 3. Серединный перпендикуляр к хорде проходит через центр окружности: EA = AF, BD⊥EF => центр O∈BD.
3. Серединный перпендикуляр к хорде проходит через центр окружности: EA = AF, BD⊥EF => центр O∈BD. 4. Отрезки касательных, исходящих из одной точки, равны: CF = CE.
4. Отрезки касательных, исходящих из одной точки, равны: CF = CE.