Выпуклый многоугольник
Многоугольник называется выпуклым, если для любых его двух точек отрезок с концами в этих точках полностью принадлежит многоугольнику. Или другими словами, многоугольник - выпуклый, если он весь располагается по одну сторону от прямой, проходящей через любые две соседние вершины.
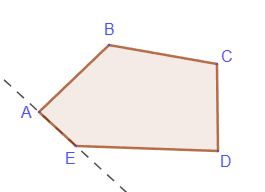
Противоположными вершинами многоугольника называются любые две вершины, не лежащие на одной его стороне. Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника:
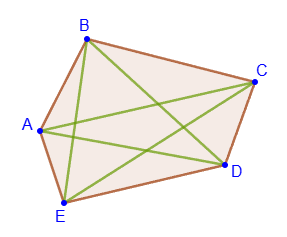
Выпуклый n-угольник - это выпуклый многоугольник, у которого n сторон. Таким образом, треугольник - это многоугольник, у которого 3 стороны, четырёхугольник - многоугольник, у которого 4 стороны и т.д.
Любой треугольник является выпуклой фигурой:
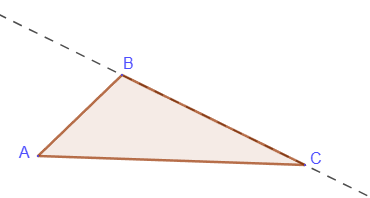
Четырехугольник может быть и выпуклым, и невыпуклым:
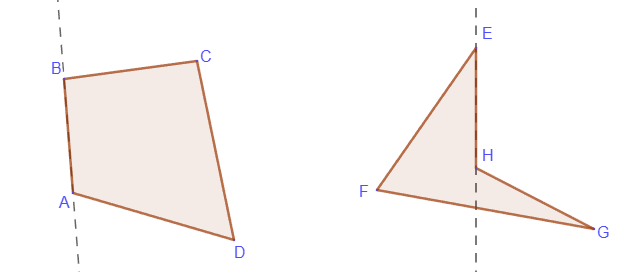
Правильный многоугольник - это выпуклый многоугольник, у которого все стороны равны и все углы равны.
В дальнейше мы будем рассматривать только выпуклые фигуры.
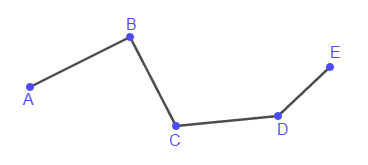Точки называются вершинами ломаной, а отрезки - звеньями.
В случае, когда конец последнего отрезка совпадает с началом первого, ломаную линию называют замкнутой:
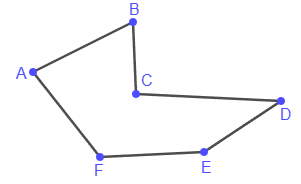Многоугольником называется часть плоскости, ограниченная замкнутой ломаной, у которой никакие два соседних отрезка не лежат на одной прямой, и никакие два не соседних отрезка не пересекаются друг с другом. Вершины и звенья ломаной называют соответственно вершинами и сторонами многоугольника.
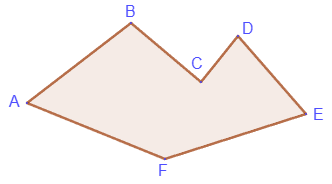Периметром многоугольника называется сумма длин всех сторон многоугольника. Половину периметра называют полупериметром.
RU