Основные теоремы об отрезках

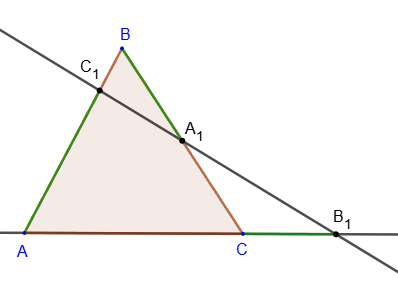
Теорема Фалеса

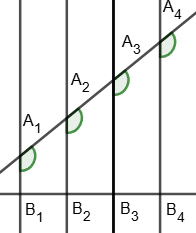
1. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой равные отрезки, отсекают равные отрезки и на другой прямой:

A₁A₂ = A₂A₃ = A₃A₄ ⇔ B₁B₂ = B₂B₃ = B₃B₄.

Теорема о пропорциональных отрезках

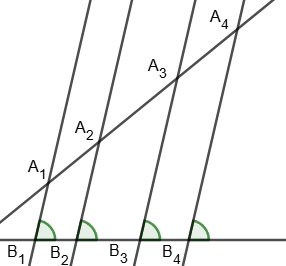
2. Параллельные прямые, пересекающие две данные прямые и отсекающие на одной прямой пропорциональные отрезки, отсекают пропорциональные отрезки и на другой прямой:

A₁A₂ : A₂A₃ : A₃A₄ = B₁B₂ : B₂B₃ : B₃B₄.

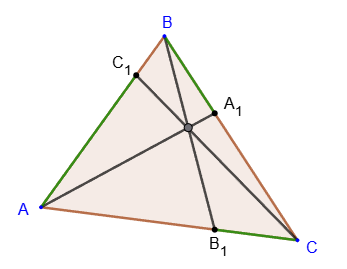
Теорема Чевы

3. Если точки A₁, B₁, C₁ лежат соответственно на сторонах BC, AC, AB треугольника ABC, причем отрезки AA₁, BB₁ и СC₁ пересекаются в одной точке, то справедливо равенство:

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1.

Обратная теорема Чевы

4. Если точки A₁, B₁, C₁ лежат соответственно на сторонах BC, AC, AB треугольника ABC, причем

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1,

то отрезки AA₁, BB₁ and СC₁ пересекаются в одной точке.

Теорема Менелая

5. Если точки A₁, B₁, C₁ лежат соответственно на сторонах BC, AC, AB треугольника ABC или на их продолжениях, то справедливо равенство

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1.

Обратная теорема Менелая

6. Если в треугольнике ABC точки A₁, B₁, C₁ лежат на сторонах AC, BC и AB или на их продолжениях, соответственно, при этом для этих точек выполняется равенство

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1,

то точки A₁, B₁, C₁ лежат на одной прямой.