Подобные треугольники
Если у треугольников ABC и A
1B
1C
1 углы соответственно равны:
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1,
то стороны, лежащие против равных углов называются сходственными:
AB and A1B1, BC and B1C1, CA and C1A1.
Два треугольника, у которых углы равны, а пары сходственных сторон пропорциональны, называются подобными.
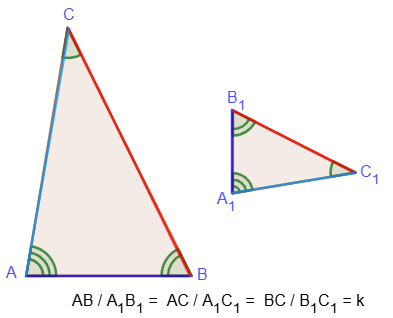
При этом коэффициент пропорциональности k называется коэффициентом подобия.
Признаки подобия треугольников
1. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
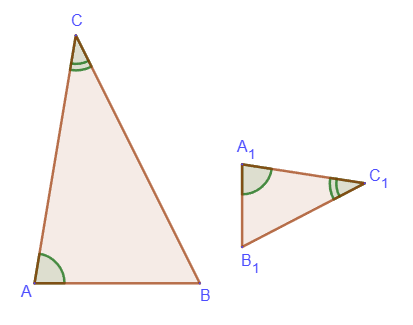
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
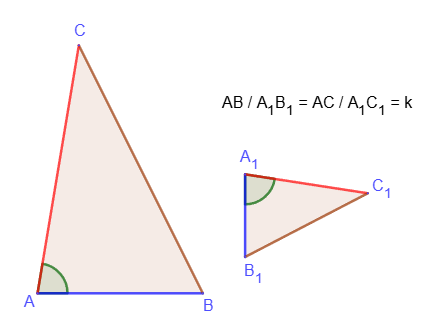
3. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
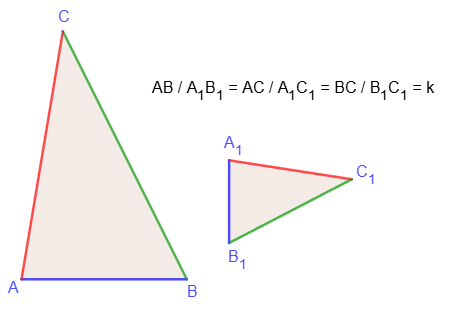
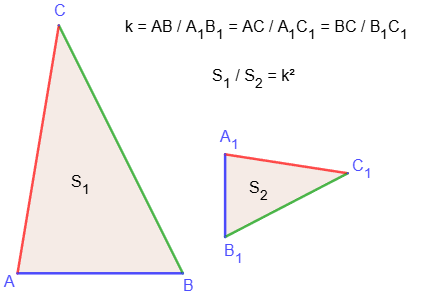
Отношение площадей подобных треугольников
Площади подобных треугольников относятся как коэффициент подобия в квадрате.
Признаки подобия прямоугольных треугольников
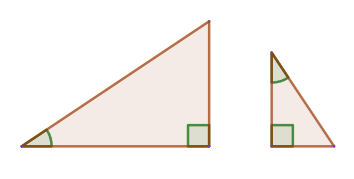
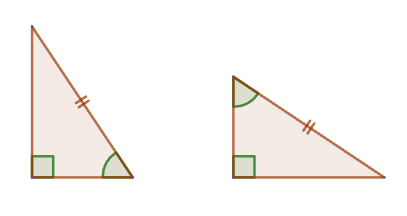
1. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.
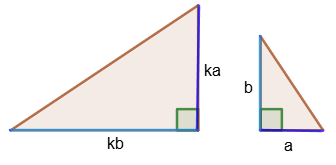
2. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
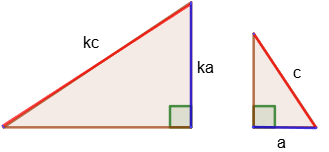
3. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
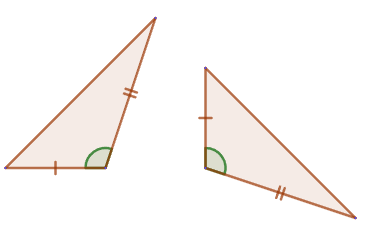 2. Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.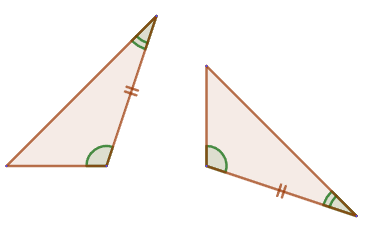 3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.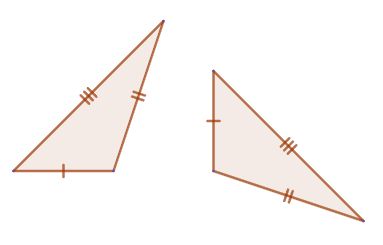
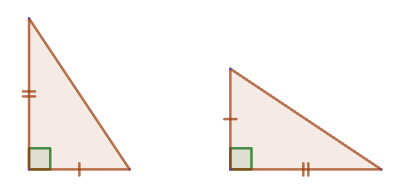 2. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.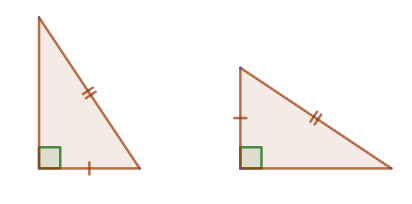 3. Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.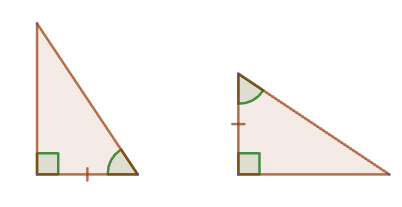
 При этом коэффициент пропорциональности k называется коэффициентом подобия.
При этом коэффициент пропорциональности k называется коэффициентом подобия. 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны. 3. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
3. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

 2. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
2. Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны. 3. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
3. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.