Сложение векторов
1. Сложение любых двух векторов по правилу треугольника.
Чтобы сложить два вектора
и
,
отложим вектор
от любой точки плоскости, а вектор
от конечной точки вектора
.
Тогда суммой векторов называется вектор
с началом в начальной точке вектора
и
конечной точкой в конечной точке вектора
:
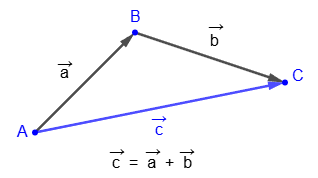
Таким образом, вектор
показывает смещение конечной точки вектора
в результате сложения с ним вектора
.
Если обозначить векторы двумя буквами, то получим правило сложения двух векторов
и
в буквенном виде:
Если обобщить этот результат на сумму нескольких векторов, то получим правило многоугольника для сложения любого числа векторов: суммой нескольких векторов называется вектор c началом в начальной точке первого вектора и концом в конечной точке последнего вектора:
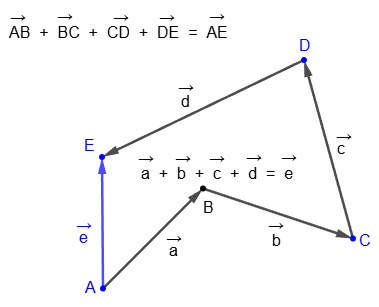
2. Сложение двух неколлинеарных векторов по правилу параллелограмма.
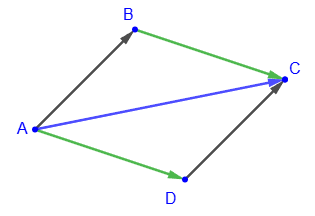
Если отложить два неколлинеарных вектора
и
от одной точки A плоскости и построить на этих векторах параллелограмм ABCD, то суммой векторов
и
будет вектор
(диагональ параллелограмма), так как
. Действительно,
 Таким образом, вектор показывает смещение конечной точки вектора в результате сложения с ним вектора .
Если обозначить векторы двумя буквами, то получим правило сложения двух векторов и в буквенном виде:
Если обобщить этот результат на сумму нескольких векторов, то получим правило многоугольника для сложения любого числа векторов: суммой нескольких векторов называется вектор c началом в начальной точке первого вектора и концом в конечной точке последнего вектора:
Таким образом, вектор показывает смещение конечной точки вектора в результате сложения с ним вектора .
Если обозначить векторы двумя буквами, то получим правило сложения двух векторов и в буквенном виде:
Если обобщить этот результат на сумму нескольких векторов, то получим правило многоугольника для сложения любого числа векторов: суммой нескольких векторов называется вектор c началом в начальной точке первого вектора и концом в конечной точке последнего вектора:
 2. Сложение двух неколлинеарных векторов по правилу параллелограмма.
2. Сложение двух неколлинеарных векторов по правилу параллелограмма.
 Если отложить два неколлинеарных вектора и от одной точки A плоскости и построить на этих векторах параллелограмм ABCD, то суммой векторов
и будет вектор (диагональ параллелограмма), так как
. Действительно,
Если отложить два неколлинеарных вектора и от одной точки A плоскости и построить на этих векторах параллелограмм ABCD, то суммой векторов
и будет вектор (диагональ параллелограмма), так как
. Действительно,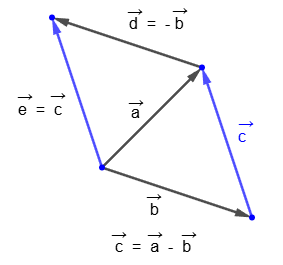
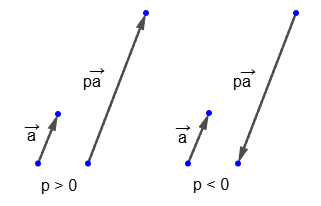 Из определения умножения вектора на число следует, что
Из определения умножения вектора на число следует, что