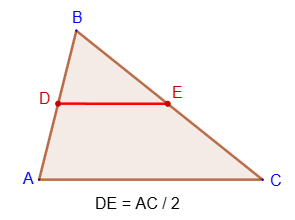
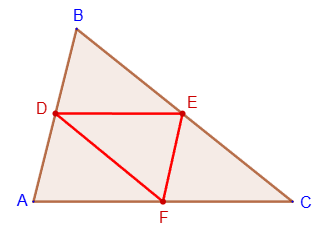
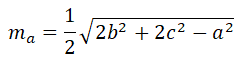Биссектриса треугольника
Биссектрисой треугольника называется отрезок
биссектрисы угла треугольника, соединяющий вершину треугольника с точкой на противоположной стороне.
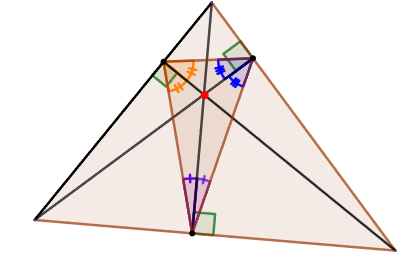
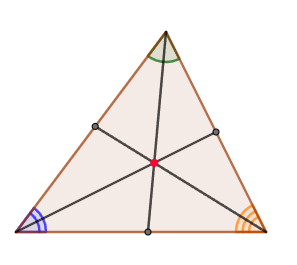
1. Биссектрисы любого треугольника пересекаются в одной точке.
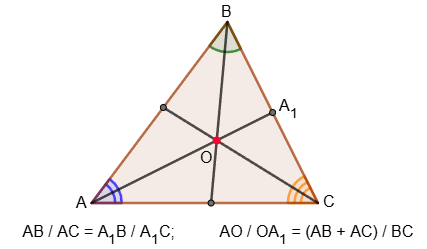
2. Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам:
AB ∕ AC = A1B ∕ A1C.
3. В треугольнике точка пересечения биссектрис делит биссектрису в отношении
AO ∕ OA1=(AB+AC) ∕ BC.
4. Длина биссектрисы l
с, проведенной к стороне c треугольника со сторонами a, b, c, равна
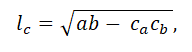
где c
a и c
b – отрезки, на которые биссектриса делит сторону c.
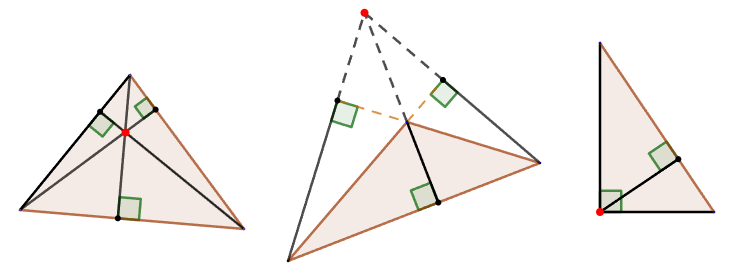
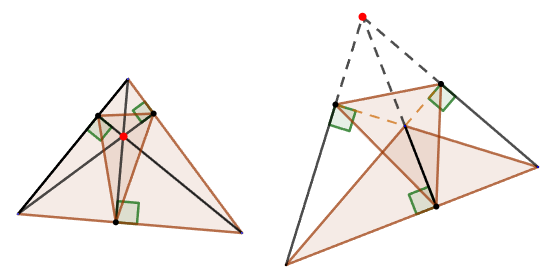
Медиана треугольника
Медианой трегольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
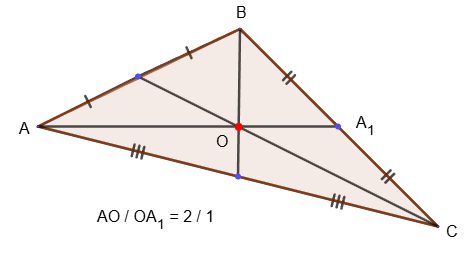
5. Медианы любого треугольника пересекаются в одной точке.
6. В треугольнике точка пересечения медиан делит медианы в отношении 2:1, считая от вершины.
7. Длина медианы m
a, проведенной к стороне a треугольника со сторонами a, b, c равна
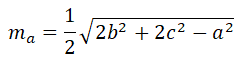
8. Медиана делит треугольник на два треугольника равной площади.
9. Три медианы делят треугольник на 6 равновеликих треугольников.


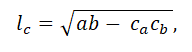 где ca и cb – отрезки, на которые биссектриса делит сторону c.
где ca и cb – отрезки, на которые биссектриса делит сторону c.