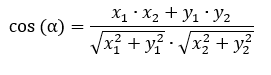Угол между векторами
Пусть даны два неколлинеарных вектора
и
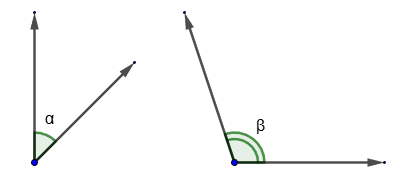
. Отложим оба эти вектора от одной точки плоскости. Углом между двумя векторами называется минимальный угол от 0° до 180°, на который надо повернуть один из них, чтобы направления векторов совпали.
Если векторы сонаправлены, то угол между ними равен 0°, если же противоположно направлены, то угол между ними равен 180°. В случае, если один из векторов или оба вектора нулевые, то угол между ними считается равным нулю.
Угол между векторами
и
обозначается
.
Скалярное произведение векторов и его свойства
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Если векторы
и
перпендикулярны, то
и, следовательно,
.
И наоборот, если
и
ненулевые, а
,
то из определения скалярного произведения следует, что
.
Таким образом, необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения.
Из определения скалярного произведения для ненулевых векторов следует, что если угол между векторами острый, то скалярное произведение - положительное число, если угол тупой - отрицательное.
Если угол между векторами равен нулю, то
.
Отсюда следует, что
2.
Если угол между векторами 180°, то
.
Очевидно, для любых векторов
,
,
и произвольного числа q скалярное произведение обладает следующими свойствами:
1)
;
2)
;
3)
.

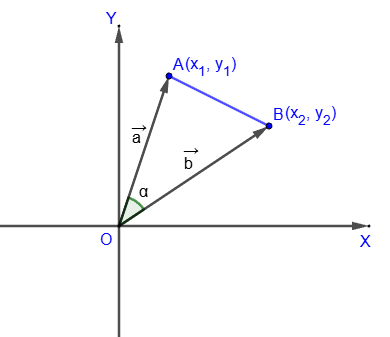 По теореме косинусов
По теореме косинусов
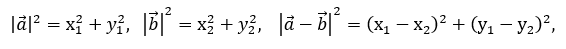 после соответствующих преобразований получим формулу для скалярного произведения в координатах:
Очевидно, что эта формула справедлива и для нулевых векторов и , и в случае коллинеарных векторов.
после соответствующих преобразований получим формулу для скалярного произведения в координатах:
Очевидно, что эта формула справедлива и для нулевых векторов и , и в случае коллинеарных векторов.