Координаты суммы и разности векторов
Пусть заданы векторы
{x
1,y
1} и
{x
2,y
2}:
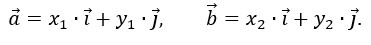
Найдем координаты {x,y} вектора
, используя геометрическое определение суммы векторов:
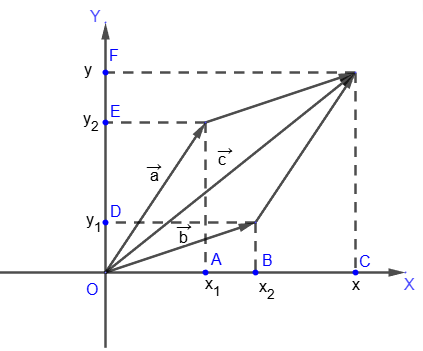
Так как AC=OB и DF=OE, то x = x
1 + x
2, y = y
1 + y
2. Таким образом, координаты суммы двух векторов равны сумме соответствующих координат этих векторов.
Можно вывести эти формулы, используя свойства сложения векторов и умножения вектора на число:
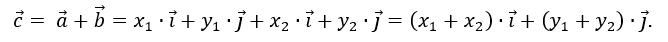
Очевидно, чтобы найти координаты суммы нескольких векторов, надо сложить соответствующие координаты этих векторов.
Аналогичным образом получаются формулы координат разности двух векторов
.
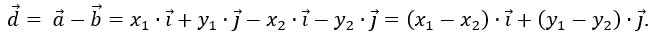
Координаты разности двух векторов равны разности соответствующих координат этих векторов.
Координаты вектора, если заданы координаты его начальной и конечной точек
Пусть заданы координаты начальной точки A(x
1, y
1) вектора
и конечной точки B(x
2, y
2).
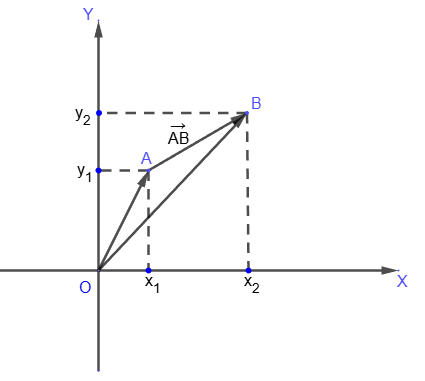
Так как
, то вектор
имеет координаты
{x2 - x1, y2 - y1}.
Таким образом, чтобы найти координаты вектора
, надо из координат конечной точки вектора вычесть соответствующие координаты начальной точки, а формула для вычисления его модуля имеет вид:
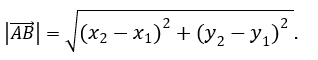
Координаты произведения вектора на число
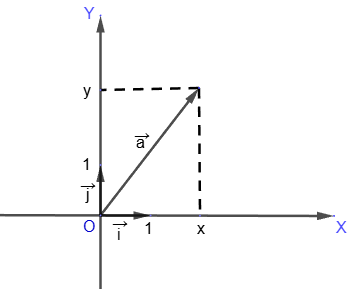
Координаты произведения вектора
{x, y} на число q равны произведениям соответствующих координат на это число:
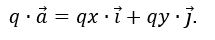
Следовательно, координаты вектора q⋅
{qx, qy}.
 Разложение нулевого вектора можно представить
Разложение нулевого вектора можно представить
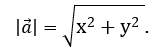
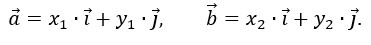 Найдем координаты {x,y} вектора , используя геометрическое определение суммы векторов:
Найдем координаты {x,y} вектора , используя геометрическое определение суммы векторов: Так как AC=OB и DF=OE, то x = x1 + x2, y = y1 + y2. Таким образом, координаты суммы двух векторов равны сумме соответствующих координат этих векторов.
Так как AC=OB и DF=OE, то x = x1 + x2, y = y1 + y2. Таким образом, координаты суммы двух векторов равны сумме соответствующих координат этих векторов.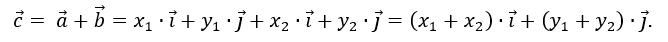 Очевидно, чтобы найти координаты суммы нескольких векторов, надо сложить соответствующие координаты этих векторов.
Очевидно, чтобы найти координаты суммы нескольких векторов, надо сложить соответствующие координаты этих векторов.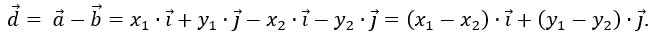 Координаты разности двух векторов равны разности соответствующих координат этих векторов.
Координаты разности двух векторов равны разности соответствующих координат этих векторов. Так как , то вектор имеет координаты
Так как , то вектор имеет координаты
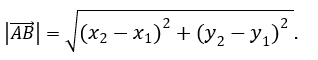
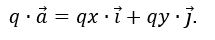 Следовательно, координаты вектора q⋅{qx, qy}.
Следовательно, координаты вектора q⋅{qx, qy}.