Координаты середины отрезка
Пусть дан отрезок AB: A=(x
1; y
1), B=(x
2; y
2). Нам нужно найти координаты (x; y) его середины - точки С.
Из точек A, B и C опустим перпендикуляры на ось X, они пересекут ось X в точках E(x
1; 0), F(x
2; 0), G(x; 0), соответственно.
По
теореме Фалеса точка G является серединой отрезка EF, то есть EG=GF.
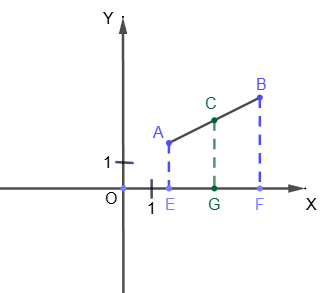
Следовательно, x-x
1=x
2-x. Отсюда получаем формулу для абсциссы точки G: x=(x
1+x
2)/2. Эта формула остается справедливой для любых случаев расположения точек A и B. Даже если AB параллельна OY, просто получаем, что абсциссы точек A, B и С совпадают.
Чтобы вывести формулу для ординаты точки C, опускаем перпендикуляры из точек A, B и C на ось OY и аналогичным образом находим, что ордината y точки G равна y=(y
1+y
2)/2.
Таким образом, формулы для координат середины отрезка имеют вид:
x=(x1+x2)/2, y=(y1+y2)/2.
Длина отрезка, расстояние между точками
Пусть дан отрезок AB: A=(x
1; y
1), B=(x
2; y
2). Нам нужно найти его длину, то есть расстояние между точками A и B.
Из точек A и B опускаем перпендикуляры на оси X и Y. Прямая, перпендикулярная оси X и проходящая через точку A, пересекает прямую, перпендикулярную оси Y и проходящую через точку B, в точке C=(x
1; y
2).
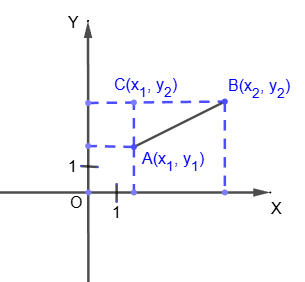
Таким образом, мы получаем прямоугольный треугольник ABC. Его гипотенузу AB найдем, используя
теорему Пифагора:
AB2 = AC2 + BC2 <=> AB2 = (y2 - y1)2 + (x2 - x1)2
Эта формула справедлива для любых случаев расположения точек A и B.
Таким образом, квадрат расстояния между двумя точками A(x
1; y
1) и B(x
2; y
2) определяется по формуле:
AB2 = (y2 - y1)2 + (x2 - x1)2
 Абсцисса точки A - это число x, абсолютная величина которого равна расстоянию от точки A до прямой OY. Если точка A расположена в правой полуплоскости, то её абсцисса x - положительное число, если в левой - отрицательное. Если точка A принадлежит оси OY, то x=0.
Абсцисса точки A - это число x, абсолютная величина которого равна расстоянию от точки A до прямой OY. Если точка A расположена в правой полуплоскости, то её абсцисса x - положительное число, если в левой - отрицательное. Если точка A принадлежит оси OY, то x=0.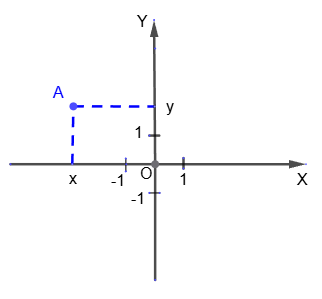
 Следовательно, x-x1=x2-x. Отсюда получаем формулу для абсциссы точки G: x=(x1+x2)/2. Эта формула остается справедливой для любых случаев расположения точек A и B. Даже если AB параллельна OY, просто получаем, что абсциссы точек A, B и С совпадают.
Следовательно, x-x1=x2-x. Отсюда получаем формулу для абсциссы точки G: x=(x1+x2)/2. Эта формула остается справедливой для любых случаев расположения точек A и B. Даже если AB параллельна OY, просто получаем, что абсциссы точек A, B и С совпадают. Таким образом, мы получаем прямоугольный треугольник ABC. Его гипотенузу AB найдем, используя теорему Пифагора:
Таким образом, мы получаем прямоугольный треугольник ABC. Его гипотенузу AB найдем, используя теорему Пифагора: