Теорема Пифагора
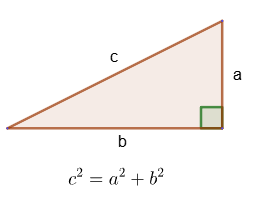
5. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Из теоремы Пифагора следует, что в любом прямоугольном треугольнике гипотенуза больше каждого из катетов.
6. Если в треугольнике квадрат одной из сторон равен сумме квадратов двух других, то такой треугольник - прямоугольный.
Прямоугольный треугольник со сторонами 3, 4, 5 часто называют египетским.
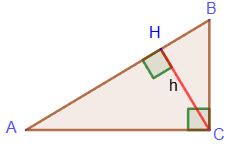
Проекции катетов на гипотенузу
Отрезки, на которые
основание высоты прямоугольного треугольника, проведенной из вершины прямого угла, делит гипотенузу, являются проекциями катетов на гипотенузу: AH - проекция катета AC на гипотенузу AB, BH - проекция катета BC на гипотенузу AB.
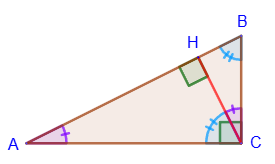
7. Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на 2 треугольника,
подобных данному: ∆ ABC∼∆ ACH∼∆ CBH.
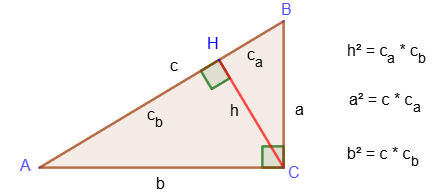
8. Квадрат длины высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению длин проекций катетов на гипотенузу.
9. Квадрат длины катета прямоугольного треугольника равен произведению гипотенузы на длину проекции этого катета на гипотенузу.
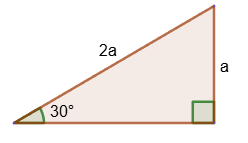 3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
4. Если в треугольнике медиана равна половине стороны, к которой проведена, то такой треугольник - прямоугольный.
3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
4. Если в треугольнике медиана равна половине стороны, к которой проведена, то такой треугольник - прямоугольный.
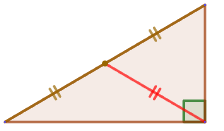

 7. Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на 2 треугольника, подобных данному: ∆ ABC∼∆ ACH∼∆ CBH.
7. Высота в прямоугольном треугольнике, проведенная из вершины прямого угла, делит его на 2 треугольника, подобных данному: ∆ ABC∼∆ ACH∼∆ CBH.
 8. Квадрат длины высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению длин проекций катетов на гипотенузу.
9. Квадрат длины катета прямоугольного треугольника равен произведению гипотенузы на длину проекции этого катета на гипотенузу.
8. Квадрат длины высоты прямоугольного треугольника, проведенной из вершины прямого угла, равен произведению длин проекций катетов на гипотенузу.
9. Квадрат длины катета прямоугольного треугольника равен произведению гипотенузы на длину проекции этого катета на гипотенузу.
