Уравнение прямой на плоскости

Общее уравнение прямой на плоскости

Общее уравнение прямой линии на плоскости - это уравнение первой степени с двумя неизвестными:

Ax + By + C = 0,

где A и B не равны 0 одновременно.
Если A=0, а B≠0, By+C=0 ⇔ y=-C/B - это уравнение прямой, параллельной оси OX.
Если A≠0, а B=0, Ax+C=0 ⇔ x=-C/A - это уравнение прямой, параллельной оси OY.
Если С=0, Ax + By = 0 - это уравнение прямой, проходящей через начало координат (0;0).

Найдем координаты точек пересечения прямой с осями координат.
Если у=0, то x=-C/A, следовательно, точка (-C/A; 0) - точка пересечения с осью OX.
Если x=0, то у=-C/B, следовательно, точка (0; -C/B) - точка пересечения с осью OY.

Уравнение прямой с угловым коэффициентом

Из общего уравнения прямой

Ax + By + C = 0

можно выразить y, если B≠0:

y = - A ∕ B ⋅ x - C ∕ B.

Таким образом, уравнение прямой можно представить в виде

y = kx + b, где k = - A ∕ B, b = - C ∕ B.

Коэффициент k называется угловым коэффициентом, так как k задает угол α наклона прямой:

k = tgα.

Здесь α - это угол между положительным направлением оси OX и прямой, отсчитываемый против часовой стрелки. Уравнение прямой с угловым коэффициентом задает любую прямую, кроме прямой, параллельной оси OY. Рассмотрим случаи расположения прямой в зависимости от значений параметров k и b.
1) Если подставить x=0 в уравнение с угловым коэффициентом, получим y=b. Следовательно, прямая y = kx + b всегда проходит через точку c координатами (0;b). Другими словами, прямая пересекает ось OY в точке (0;b). Если b=0, то уравнение принимает вид y=kx, и прямая проходит через начало координат - точку (0;0).
Если b>0, то прямая пересекает ось OY в верхней полуплоскости, если b<0, то в нижней.


2) Если α=0, то k=tgα=0, и уравнение прямой принимает вид y=b. Её график представляет собой прямую, параллельную оси OX. Если k=0, b=0, прямая совпадает с осью OX.
Если α - острый угол, то k=tgα>0, и уравнение y=kx+b задаёт возрастающую функцию.
Если α - тупой угол, то k=tgα<0, и уравнение y=kx+b задаёт убывающую функцию.

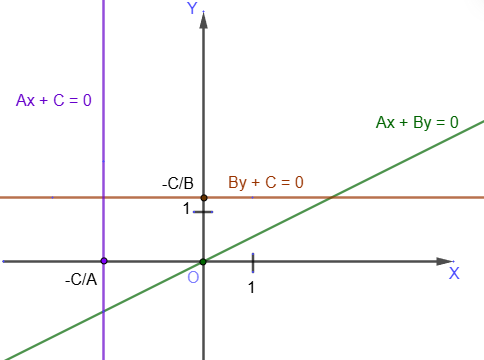
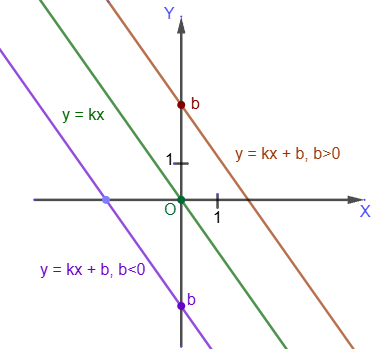
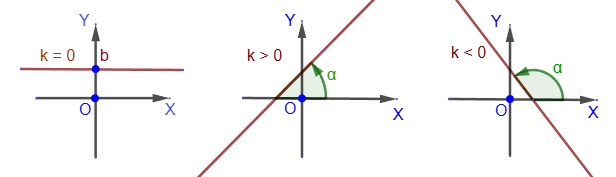
Уравнение прямой, проходящей через заданную точку

Пусть задана точка P(x₀; y₀). Подставим координаты точки P в уравнение прямой y=kx+b:

y₀ = kx₀ + b   ⇔    b = y₀ - kx₀.

Подставляя найденное значение b в уравнение, получим:

y = kx + y₀ - kx₀   ⇔   y = k(x - x₀) + y₀   ⇔   y - y₀ = k(x - x₀).

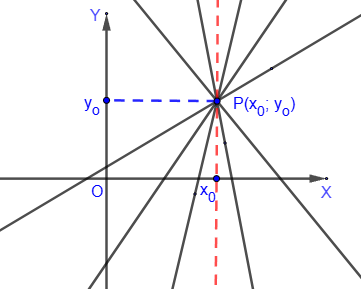
Это уравнение прямой задает пучок прямых (кроме вертикальной прямой) с центром в точке P(x₀; y₀):

Уравнение прямой, проходящей через две заданные точки

Пусть заданы две точки P₁(x₁; y₁) и P₂(x₂; y₂). Получим уравнение прямой, проходящей через эти точки.
Уравнение пучка прямых с центром в точке P₁(x₁; y₁):

y - y₁ = k(x - x₁).

Чтобы из этого уравнения получить уравнение прямой, проходящей через точку P₂(x₂; y₂), нужно найти соответствующий угловой коэффициент . Для этого просто подставим координаты точки P₂ в уравнение пучка:

y₂ - y₁ = k(x₂ - x₁)   ⇔   k = (y₂ - y₁) ∕ (x₂ - x₁).

И окончательно, получаем

y - y₁ = (y₂ - y₁) ∕ (x₂ - x₁)⋅(x - x₁).

Обычно уравнение прямой, проходящей через две точки, записывают в виде:

(y - y₁) ∕ (y₂ - y₁) = (x - x₁) ∕ (x₂ - x₁).

При этом угловой коэффициент прямой k = (y₂ - y₁) ∕ (x₂ - x₁).
Если заданные точки P₁ и P₂ лежат на прямых, параллельных осям координат, то есть y₂ = y₁ ( || оси OX) или x₂ = x₁ ( || оси OY), уравнения прямых будут, соответственно, y = y₁ или x = x₁.

Условия параллельности и перпендикулярности двух прямых

1) Две прямые y=k₁x+b₁ и y=k₂+b₂ параллельны тогда и только тогда, когда их угловые коэффициенты совпадают k₁=k₂.
2) Получим условие перпендикулярности прямых. Рассмотрим две прямые с угловыми коэффициентами k₁=tgα₁ и k₂=tgα₂. Необходимое и достаточное условие их перпендикулярности:

α₁ - α₂ = π/2   ⇔   α₁ = α₂+π/2   ⇔   tgα₁ = tg(α₂+π/2)   ⇔   tgα₁ = -ctgα₂ ⇔ k₁k₂ = -1.

Таким образом, мы получили необходимое и достаточное условие перпендикулярности двух прямых: произведение угловых коэффициентов должно быть равно   -1.

Угол между двумя прямыми

Найдем угол α между двумя прямыми AC и BC, заданными уравнениями y=k₁x+b₁, y=k₂+b₂. Считаем, что прямые не перпендикулярны.
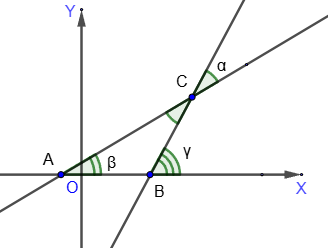
Угол ∠ACB=∠α, так как эти углы вертикальные. Поскольку угол γ - внешний угол треугольника ABC,

γ = α + β ⇔ α = γ - β.

Следовательно, используя известную тригонометрическую формулу, получаем:

tgα = tg(γ - β)   ⇔   tgα = (tgγ - tgβ) ∕ (1 + tgγ tgβ).

Так как tgβ = k₁, tgγ = k₂,

tgα = (k₁ - k₂) ∕ (1 + k₁k₂).

Углом между двумя прямыми по определению считается острый угол (или прямой, если прямые перпендикулярны), следовательно, tgα≥0. Поэтому формула для тангенса угла между прямыми имеет вид:

tgα = |(k₁ - k₂) ∕ (1 + k₁k₂)|.

Если прямые AC и BC перпендикулярны, то k₁k₂=-1, и в этом случае формула не имеет смысла.
Также формула не имеет смысла, если хотя бы одна из прямых параллельна оси OY. В этом случае угол между прямыми легко найти из соображений здравого смысла по формуле α=|π/2-β| или α=|π/2-γ|.

Условие, при котором три заданных точки лежат на одной прямой

Пусть заданы три точки P₁(x₁; y₁), P₂(x₂; y₂) и P₃(x₃; y₃). Запишем уравнение прямой, прходящей через две точки P₁ и P₂:

(y - y₁) ∕ (y₂ - y₁) = (x - x₁) ∕ (x₂ - x₁).

Чтобы точка P₃ лежала на этой прямой, необходимо и достаточно, чтобы её координаты удовлетворяли этому уравнению. Поэтому просто подставим координаты x₃, y₃ точки P₃ в уравнение прямой и получим условие, при котором три точки лежат на одной прямой:

(y₃ - y₁) ∕ (y₂ - y₁) = (x₃ - x₁) ∕ (x₂ - x₁).