Трапеция

Трапеция это четырехугольник, у которого две стороны параллельны, а две другие не параллельны:
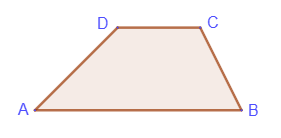
Параллельные стороны трапеции называются основаниями (AB - нижним основанием, СD - верхним основанием), а не параллельные стороны AD и BC - боковыми сторонами.
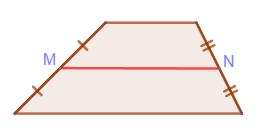
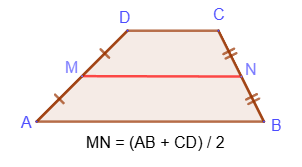
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон трапеции:
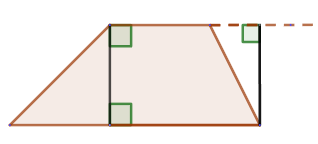
Высотой трапеции называют перпендикуляр, опущенный из любой точки одного из оснований трапеции на другое основание или его продолжение:

Типы трапеций

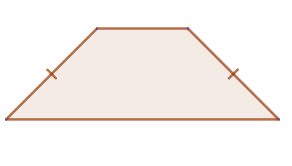
1. Трапеция называется равнобокой или равнобедренной, если её боковые стороны равны:
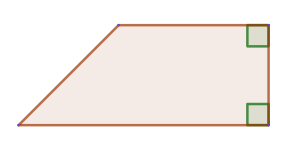
2. Трапеция называется прямоугольной, если один из её углов - прямой:

Свойства трапеции

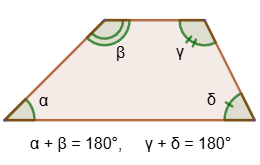
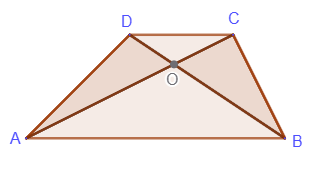
1. Средняя линия трапеции параллельна её основаниям и равна их полусумме: 2. Сумма углов, прилежащих к боковой стороне трапеции, равна 180°: 3. Треугольники, образованные при пересечении диагоналей, и содержащие основания, подобны:

ΔAOB∾ΔCOD, k = AB/CD=AO/OC=BO/OD

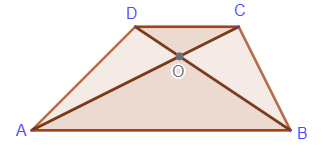
4. Треугольники, образованные при пересечении диагоналей, и содержащие боковые стороны, имеют равные площади:

S_ΔADC=S_ΔBCD, S_ΔADO=S_ΔBCO, S_ΔADB=S_ΔBCA

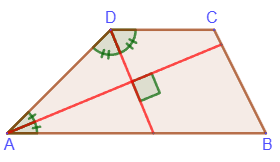
5. Биссектрисы углов при боковой стороне трапеции перпендикулярны:
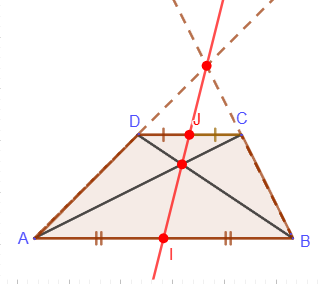
6. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой:
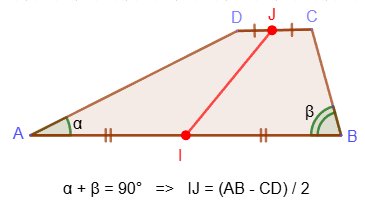
7. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности:

Свойства равнобедренной трапеции

1. Углы равнобедренной трапеции при каждом из её оснований равны:
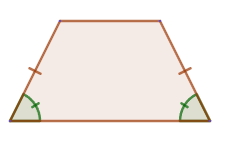2. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований: DH=(AB+CD)/2.
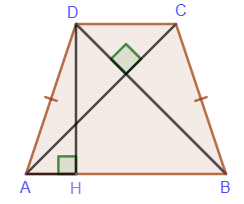3. Если трапеция является равнобедренной, то около неё можно описать окружность: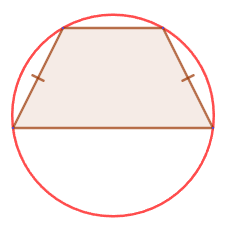

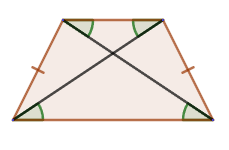Признаки равнобедренной трапеции

1. Если у трапеции диагонали равны, то она является равнобедренной.
2. Если диагонали трапеции образуют равные углы с одним из оснований, то диагонали образуют равные углы и с другим основанием, а трапеция является равнобедренной:
3. Если около трапеции можно описать окружность, то она является равнобедренной.