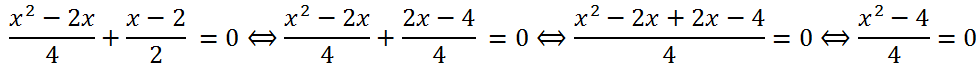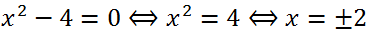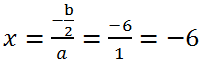Уравнение вида
ax2 + bx + c = 0, где
a, b, c – некоторые числа, причем
a ≠ 0, называется квадратным. Многочлен
ax2 + bx + c обычно называют квадратным трехчленом.
Квадратное уравнение называется полным, если коэффициенты
b и
c отличны от нуля.
Неполное квадратное уравнение – уравнение, у которого либо
b = 0, либо
с = 0, либо и
b = 0, и
с = 0 одновременно. Следовательно, неполные квадратные уравнения имеют вид
ax2 = 0, либо
ax2 + с = 0, либо
ax2 + bx = 0.
Приведенным квадратным уравнением называется уравнение, у которого коэффициент
a = 1, то есть уравнения вида
x2 + px + q = 0.
Решение неполных квадратных уравнений
Решение полных квадратных уравнений
Теорема Виета и ее применение для решения квадратных уравнений
Решение биквадратных уравнений
Примеры решения квадратных уравнений
Пример 1.
Решить квадратное уравнение
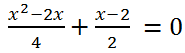 Решение.
Решение.
Приведем к общему знаменателю левую часть уравнения:
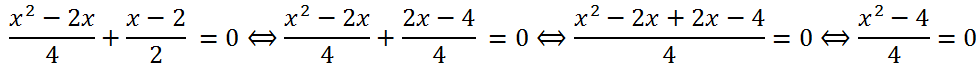
Умножим на 4 обе части уравнения:
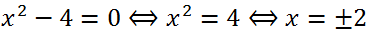 Ответ:
Ответ: -2, 2.
Пример 2.
Решить квадратное уравнение x
2 + 3x + 10 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 3, c = 10.
D = b
2 - 4ac = 3
2 - 4*1*10 = 9 - 40 = -31 < 0, следовательно, действительных корней нет.
Ответ: корней нет.
Пример 3.
Решить квадратное уравнение x
2 + 12x + 36 = 0.
Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 12, c = 36.
Так как b = 12 - четное число, то вычислим дискриминант D
1 :
D
1 = (
)
2 - ac = 6
2 - 1*36 = 0, следовательно, уравнение имеет единственный корень
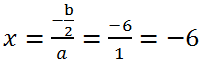
Это уравнение можно решить и без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
x
2 + 12x + 36 = 0 <=> (x + 6)
2 = 0 <=> x = -6.
Ответ: -6.
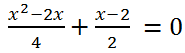 Решение.
Решение.