Особенности уравнения окружности
Если мы раскроем скобки в уравнении окружности, то получим следующее уравнение второго порядка:
x2 + y2 - 2ax - 2by + a2 + b2 - R2 = 0.
Таким образом, легко видеть, что коэффициенты при x
2 и y
2 равны 1 и отсутствует член, содержащий произведение xy.
Рассмотрим уравнение второго порядка вида:
Ax2 + Ay2 + Bx + Dy + E = 0.
Разделим обе его части на A и выделим полные квадраты:
x2 + y2 + B/A⋅x + D/A⋅y + E/A = 0 ⇔
⇔ (x2 + 2B/(2A)⋅x + B2/(4A2)) + (y2 + 2D/(2A)⋅y + D2/(4A2)) + E/A - B2/(4A2) - D2/(4A2) = 0 ⇔
⇔ (x + B/(2A))2 + (y + D/(2A))2 = (B2 + D2 - 4AE) / (4A2).
Обозначив B/(2A)=-a, D/(2A)=-b, правую часть последнего уравнения (B
2+D
2-4AE) / (4A
2) = F, получим уравнение:
(x - a)2 + (y - b)2 = F.
Рассмотрим три случая для значения правой части уравнения F: F>0, F=0 и F<0.
1) Если F>0, то уравнение определяет окружность с центром в точке (a; b) и радиусом R=√F.
2) Если F=0, то уранение принимает вид (x - a)
2 + (y - b)
2 = 0 и определяет единственную точку с координатами (a; b).
3) Если F<0, то уравнение не имеет действительных корней. Его решениями будут только
комплексные числа, и уравнение в этом случае называется уравнением мнимой окружности.
Примеры определения координат центра и радиуса окружности, заданной уравнением второго порядка
1) x
2 + y
2 - 10x + 4y + 20 = 0
Это уравнение можно преобразовать следующим образом:
(x2 - 10x + 25) + (y2 + 4y + 4) + 20 - 25 - 4 = 0 ⇔ (x - 5)2 + (y + 2)2 = 9
Последнее уравнение определяет окружность, центр которой находится в точке (5;-2), а радиус R=3.
2) 3x
2 + 3y
2 + 6x - 12y + 8 = 0
Преобразуем это уравнение к виду:
3(x2 + 2x + 1) + 3(y2 - 4y + 4) + 8 - 3 - 12 = 0 ⇔ 3(x + 1)2 + 3(y - 2)2 = 7
Разделив последнее уравнение на 3, получим
(x + 1)2 + (y - 2)2 = 7/3
Последнее уравнение определяет окружность, центр которой находится в точке (-1;2), а радиус R=√7/3.
3) x
2 + y
2 - 16x - 2y - 15 = 0
Преобразуем это уравнение к виду:
(x - 8)2 + (y - 1)2 = -50
Это уравнение не имеет действительных корней и определяет мнимую окружность.
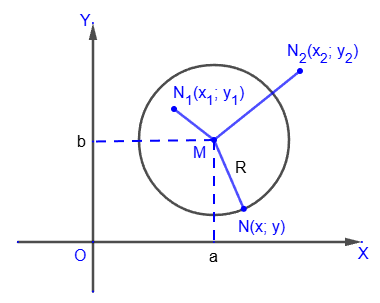
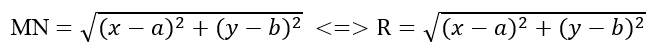 Возведя последнее уравнение в квадрат, получим уравнение окружности:
Возведя последнее уравнение в квадрат, получим уравнение окружности:
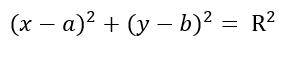 Этому уравнению удовлетворяют только те точки, которые принадлежат этой окружности.
Этому уравнению удовлетворяют только те точки, которые принадлежат этой окружности.