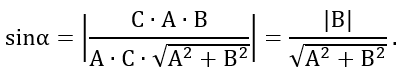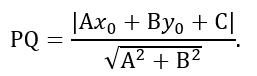Пусть задана произвольная точка P(x
0; y
0) и прямая MN: Ax + By + C = 0.
Получим формулу для расстояния d от точки P до прямой MN. Запишем уравнение прямой как уравнение с угловым коэффициентом:
y = - A ∕ B ⋅ x - C ∕ B.
Найдем координаты точек пересечения этой прямой с осями координат:
M: x=0 => y = - C ∕ B => M(0; - C ∕ B).
N: y=0 => x = - C ∕ A => N(- C ∕ A; 0).
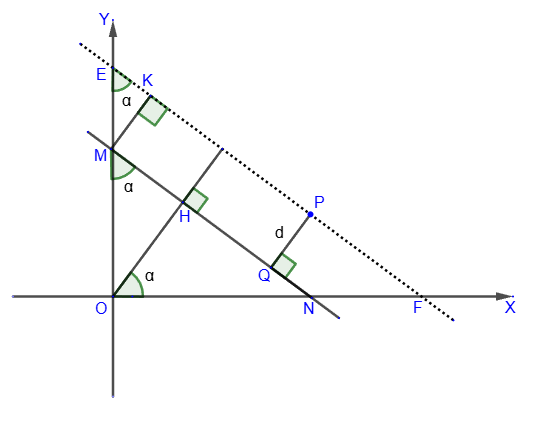
Проведем прямую EF || MN через точку P. Используя
уравнение прямой, проходящей через заданную точку,
и условие
параллельности прямых, получаем уравнение прямой EF в виде:
y = - A ∕ B ⋅ x + y0 + A ∕ B ⋅ x0.
Расстояние между параллельными прямыми MN и EF равно расстоянию от точки P до прямой MN, то есть PQ=MK=d.
Пусть ∠NOH=α, тогда ∠NOH=∠MEK=α, как
углы с соответственно перпендикулярными сторонами.
Так как ΔEKM - прямоугольный, по определению
синуса угла
sinα = MK / ME ⇔ MK = ME⋅sinα.
Координаты точки M(0;- C ∕ B), а точки E(0; y
0 + A ∕ B ⋅ x
0), следовательно,
длина отрезка ME равна:
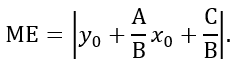
 Получим формулу для расстояния d от точки P до прямой MN. Запишем уравнение прямой как уравнение с угловым коэффициентом:
Получим формулу для расстояния d от точки P до прямой MN. Запишем уравнение прямой как уравнение с угловым коэффициентом:
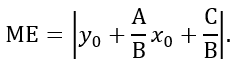
 Прямоугольный ΔMON подобен прямоугольному ΔHON, следовательно,
Прямоугольный ΔMON подобен прямоугольному ΔHON, следовательно,